已知函数 ,
, 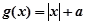
(1)当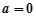 时,解不等式
时,解不等式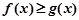 ;
;
(2)若存在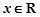 ,使得
,使得 成立,求实数
成立,求实数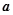 的取值范围.
的取值范围.
如图,在四棱锥 中,
中, 平面
平面 ,
, 平面
平面 ,
, ,
, .
.
(Ⅰ)求证:平面 平面
平面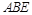 ;
;
(Ⅱ)求二面角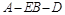 的大小.
的大小.
(本小题满分12分)甲、乙等 名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为
名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为 ).
).
(Ⅰ)求甲、乙两考生的面试序号至少有一个为奇数的概率;
(Ⅱ)记在甲、乙两考生之间参加面试的考生人数为 ,求随机变量
,求随机变量 的分布列与期望.
的分布列与期望.
已知函数 的最小正周期为
的最小正周期为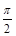 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)设 的三边
的三边 满足
满足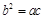 ,且边
,且边 所对的角为
所对的角为 ,求此时函数
,求此时函数 的值域.
的值域.
已知函数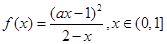 ,它的一个极值点是
,它的一个极值点是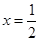 .
.
(Ⅰ) 求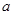 的值及
的值及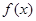 的值域;
的值域;
(Ⅱ)设函数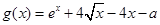 ,试求函数
,试求函数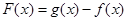 的零点的个数.
的零点的个数.
已知椭圆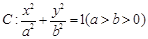 的离心率为
的离心率为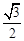 ,且经过点
,且经过点 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)如果过点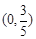 的直线与椭圆交于
的直线与椭圆交于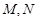 两点(
两点(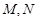 点与
点与 点不重合),
点不重合),
①求 的值;
的值;
②当 为等腰直角三角形时,求直线
为等腰直角三角形时,求直线 的方程.
的方程.