如图①在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E,F,G分别是线段PC、PD,BC的中点,现将ΔPDC折起,使平面PDC⊥平面ABCD(如图②)
(1)求证AP∥平面EFG;
(2)求直线AP与平面EFG之间的距离;
(3)在线段PB上确定一点Q,使PC⊥平面ADQ,试给出证明.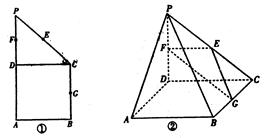
在1L高产小麦种子中混入了一粒带麦锈病的种子,从中随机抽取10mL,含有麦锈病种子的概率是多大?
小明家的晚报在下午5:30~6:30之间的任何一个时间随机地被送到,小明家一家人在下午6:00~7:00之间的任何一个时间随机地开始晚餐。
(1)你认为晚报在晚餐开始之前被送到和在晚餐开始之后被送到哪一种可能性更大?
(2)晚报在晚餐开始之前被送到的概率是多大?
取一根长度为3m的绳子,拉直后在任意位置剪断,则剪得的两段的长度都不小于1m的概率有多大?
一海豚在水池中自由游弋。水池为长30m、宽20 m的长方形。求此刻海豚嘴尖离岸边不超过2m的概率。
平面上画了一些彼此相距2a的平行线,把一枚半径r<a的硬币任意掷在这平面上,求硬币不与任一条平行线相碰的概率。