给定抛物线C:y2=4x,F是C的焦点,过点F的直线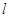 与C相交于A、B两点。
与C相交于A、B两点。
(1)设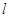 的斜率为1,求
的斜率为1,求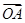 与
与 夹角的余弦值;
夹角的余弦值;
(2)设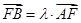 ,若
,若 ∈[4,9],求
∈[4,9],求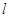 在y轴上截距的变化范围。
在y轴上截距的变化范围。
(本小题满分12分)
已知函数 ,
,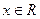 的最大值是1且其图像经
的最大值是1且其图像经 过点
过点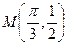 (1)求
(1)求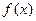 的解析式;
的解析式;
(2)已知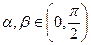 ,且
,且 ,
, 求
求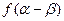 的值.
的值.
(本小题满分14分)
已知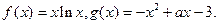
(1)求函数 上的最小值;
上的最小值;
(2)对一切 恒成立,求实数
恒成立,求实数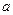 的取值范围;
的取值范围;
(3)证明:对一切 ,都有
,都有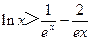 成立.
成立.
(本小题满分12分)
已知实轴长为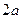 ,虚轴长为
,虚轴长为 的双曲线
的双曲线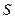 的焦点在
的焦点在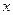 轴上,直线
轴上,直线 是双曲线
是双曲线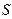 的一条渐近线,且原点
的一条渐近线,且原点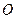 、点
、点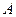
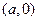 和点
和点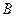
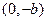 )使等式
)使等式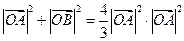 成立.
成立.
(I)求双曲线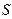 的方程;
的方程;
(II)若双曲线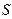 上存在两个点关于直线
上存在两个点关于直线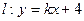 对
对 称,求实数
称,求实数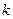 的取值范围.
的取值范围.
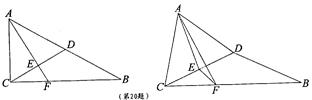
如图,在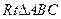 中,
中,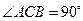 ,
,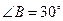 ,
,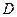 、
、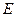 分别为
分别为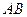 、
、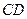 的中点,
的中点,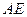 的延长线交
的延长线交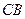 于
于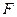 。现将
。现将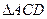 沿
沿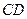 折起,折成二面角
折起,折成二面角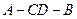 ,连接
,连接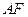 .
.
(I)求证 :平面
:平面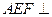 平面
平面 ;
;
(II)当
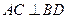 时,求二面角
时,求二面角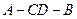 大小的余弦值.
大小的余弦值.
(本小题满分12分)
已知各项均为正数的数列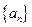 满足
满足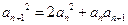 , 且
, 且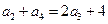 ,
,
其中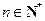 .
.
(I)求数列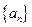 的通项公式;
的通项公式;
(II)设 数列
数列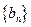 的前
的前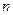 项和为
项和为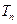 ,令
,令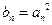 ,其中
,其中 ,试比较
,试比较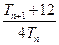 与
与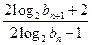 的大小,并加以证明.
的大小,并加以证明.