(本小题满分14分)某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为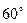 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为 平方米,且高度不低于
平方米,且高度不低于 米.记防洪堤横断面的腰长为
米.记防洪堤横断面的腰长为 (米),外周长(梯形的上底线段
(米),外周长(梯形的上底线段 与两腰长的和)为
与两腰长的和)为 (米).
(米).
⑴求 关于
关于 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
⑵要使防洪堤横断面的外周长不超过 米,则其腰长
米,则其腰长 应在什么范围内?
应在什么范围内?
⑶当防洪堤的腰长 为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.
为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值. 
(本小题满分14分)
如图,在四棱锥 中,
中, ,
,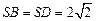 ,底面
,底面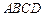 是菱形,且
是菱形,且 ,
,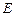 为
为 的中点.
的中点.
(Ⅰ)证明: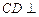 平面
平面 ;
;
(Ⅱ)侧棱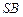 上是否存在点
上是否存在点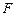 ,使得
,使得 平面
平面 ?并证明你的结论.
?并证明你的结论.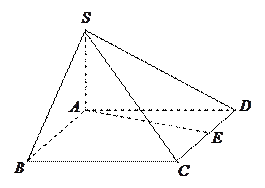
(本小题满分14分)
设某旅游景点每天的固定成本为500元,门票每张为30元,变动成本与购票进入旅游景点的人数的算术平方根成正比。一天购票人数为25时,该旅游景点收支平衡;一天购票人数超过100时,该旅游景点须另交保险费200元。设每天的购票人数为 ,盈利额为
,盈利额为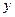 元。
元。
(Ⅰ)求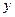 与
与 之间的函数关系;
之间的函数关系;
(Ⅱ)该旅游景点希望在人数达到20人时即不出现亏损,若用提高门票价格的措施,则每张门票至少要多少元(取整数)?
(参考数据: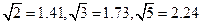 .)
.)
(本小题满分12分)
从1、2、3、4、5、8、9这7个数中任取三个数,共有35种不同的取法(两种取法不同,指的是一种取法中至少有一个数与另一种取法中的三个数都不相同)。
(Ⅰ)求取出的三个数能够组成等比数列的概率;
(Ⅱ)求取出的三个数的乘积能被2整除的概率。
(本小题满分12分)
已知向量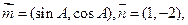 且
且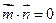 。
。
(Ⅰ)求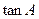 的值;
的值;
(Ⅱ)求函数 的值域。
的值域。
已知抛物线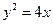 及点
及点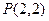 ,直线
,直线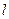 斜率为
斜率为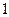 且不过点
且不过点 ,与抛物线交于点
,与抛物线交于点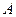 、
、 两点.
两点.
(Ⅰ)求直线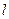 在
在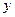 轴上截距的取值范围;
轴上截距的取值范围;
(Ⅱ)若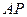 、
、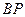 分别与抛物线交于另一点
分别与抛物线交于另一点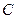 、
、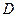 ,证明:
,证明: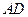 、
、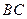 交于定点.
交于定点.