已知△ABC三边所在直线方程为 ,
, ,
, ,
, 为坐标原点。
为坐标原点。
(1)求 边上的高所在的直线方程;
边上的高所在的直线方程;
(2)若直线 经过点
经过点 ,且交
,且交 轴负半轴于点
轴负半轴于点 ,交
,交 轴正半轴于点
轴正半轴于点 ,
, 的面积为
的面积为 ,求
,求 的最小值并求此时直线
的最小值并求此时直线 的方程
的方程
已知二次函数 满足条件
满足条件 ,及
,及 .
.
(1)求 的解析式;
的解析式;
(2)求 在
在 上的最值.
上的最值.
已知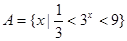 ,
, .
.
(1)求 和
和 ;
;
(2)定义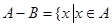 且
且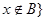 ,求
,求 和
和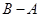 .
.
某城市2001年末汽车保有量为30万辆,预计此后每年报废上一年末汽车保有量的6%,并且每年新增汽车数量相同.为保护城市环境,要求该城市汽车保有量不超过60万辆,那么每年新增汽车数量不应超过多少辆?
等比数列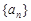 的首项为
的首项为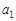 ,公比为
,公比为 ,用
,用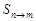 表示这个数列的第n项到第m项共
表示这个数列的第n项到第m项共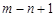 项的和.
项的和.
(Ⅰ)计算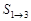 ,
,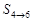 ,
, ,并证明它们仍成等比数列;
,并证明它们仍成等比数列;
(Ⅱ)受上面(Ⅰ)的启发,你能发现更一般的规律吗?写出你发现的一般规律,并证明.
已知数列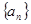 是公比为
是公比为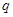 的等比数列,
的等比数列,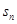 是其前
是其前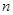 项和,且
项和,且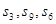 成等差数列
成等差数列
(1)求证: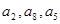 也成等差数列
也成等差数列
(2)判断以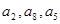 为前三项的等差数列的第四项是否也是数列
为前三项的等差数列的第四项是否也是数列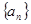 中的一项,若是求出这一项,若不是请说明理由.
中的一项,若是求出这一项,若不是请说明理由.