如图，在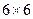
的正方形网格中，每个小正方形的边长都为1，请在所给网格中按下列要求画出图形．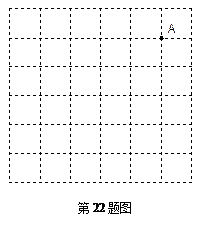
从点A出发的一条线段AB，使它的另一个端点落在格点（即小正方形的顶点）上，且长度为
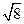
以（1）中的AB为边的一个等腰ABC，使点C在格点上，且另两边的长都是无理数（画出一个符合条件的三角形即可）
画出（2）中△ABC关于点B的中心对称图形△A1BC1.
（1）解方程
（2）化简：
－
+
一个长方体水箱，从里面量长25厘米,宽20厘米,深30厘米,水箱里已经盛有深为a厘米的水。现在往水箱里放进一个棱长10厘米的正方体实心铁块（铁块底面紧贴水箱底部）。
（1）如果
，则现在的水深为 cm。
（2）如果现在的水深恰好和铁块高度相等，那么a是多少？
（3）当
时，现在的水深为多少厘米?（用含a的代数式表示，直接写出答案）
小明的爸爸骑着摩托车带着小明在公路上匀速行驶，小明每隔一段时间看到的里程碑上的数（单位：公里）如下：
设小明12：00时看到的两位数的个位数字为x。
（1）小明12：00时看到的两位数的十位数字为。（用x表示）
（2）小明13：00时看到的两位数为； 14：30时看到的两位数为；（用x表示，需要化简）。
(3) 你能帮助小明求出摩托车的速度吗？试试看。
在一条数轴上有A、B两点，点A表示数
，点B表示数6。点P是该数轴上的一个动点（不与A、B重合）表示数x。点M、N分别是线段AP、BP的中点。
（1）如果点P在线段AB上，则点M表示的数是 , 则点N表示的数是（用含x 的代数式表示）。并计算线段MN的长。
（2）如果点P在点B右侧，请你计算线段MN的长。
（3）如果点P在点A左侧，则线段MN的长度会改变吗？如果改变，请说明理由；如果不变，请直接写出结果。
列方程解应用题：甲、乙两班共有98人，若从甲班调3人到乙班，那么两班人数正好相等。那么甲班原有多少人？