(本小题满分12分)若圆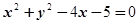 与圆
与圆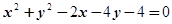
交点为A,B,求:(1) 线段AB的垂直平分线方程.
(2) 线段AB所在的直线方程.
(3) 求AB的长.
(本小题满分12分)在直角坐标平面上有一点列 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数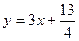 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以 为首项,-1为公差的等
为首项,-1为公差的等 差数列{xn}.
差数列{xn}.
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0, ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求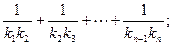
(3) 设
设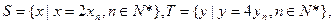 等差数列
等差数列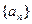 的任一项
的任一项 ,其中
,其中 是
是 中的最大数,
中的最大数, ,求数列
,求数列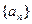 的通项公式.
的通项公式.
(本小题满分12 分)已知曲线C上任意一点M到点F(0,1)的距离比它到直线
分)已知曲线C上任意一点M到点F(0,1)的距离比它到直线 的距离小1.
的距离小1.
(1)求曲线C的方程;
(2)过点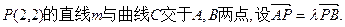 当△AOB的面积为
当△AOB的面积为 时(O为坐标原点),求
时(O为坐标原点),求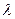 的值.
的值.
(本小题满分12分)设函数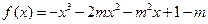 (其中
(其中 )的图象在
)的图象在 处的切线与直线
处的切线与直线 平行.
平行.
(1)求 的值;
的值;
(2)求函数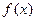 在区间[0,1]的最小值;
在区间[0,1]的最小值;
(3)若 ,
, ,
,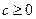 ,且
,且 ,
,
试根据上述(Ⅰ)、(Ⅱ)的结论证 明:
明: .
.
(本小题满分12分)如图,正三棱柱 所有棱
所有棱 长都是
长都是 ,
,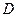 是棱
是棱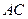 的中点,
的中点,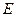 是棱
是棱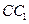 的中点,
的中点,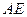 交
交 于点
于点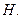
(1)求证: ;
;
(2)求二面角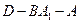 的大小(用反三角函数表示);
的大小(用反三角函数表示);
(3)求点 到平面
到平面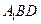 的距离.
的距离.
(本小题满分12分)设在12个同类型的零件中有2个次品,抽取3次进行检验,每次任取一个,并且取出不再放回,若以 表示取出次品的个数. 求
表示取出次品的个数. 求 的分布列,期望及方差.
的分布列,期望及方差.