（本小题满分12分）
某中学举办安全法规知识竞赛，从参赛的高一、高二学生中各抽出100人的成绩作为样本。对高一年级的100名学生的成绩进行统计，并按[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]分组，得到成绩分布的频率分布直方图（如图）。
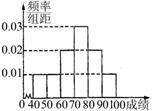
（Ⅰ）若规定60分以上（包括60分）为合格，计算高一年级这次知识
赛的合格率；
（Ⅱ）若高二年级这次知识竞赛的合格率为60%，由以上统计数据填写下 面2×2列联表，并问是否有99%的把握认为“这次知识竞赛的成绩与年级有关系”。
| |
高一 |
高二 |
合计 |
| 合格人数 |
|
|
|
| 不合格人数 |
|
|
|
| 合计 |
|
|
|
参考数据与公式：
由列联表中数据计算
临界值表
| P（K≥k0） |
0.10 |
0.05 |
0.010 |
| k0 |
2.706 |
3.841 |
6.635 |
（本小题满分12分）
已知函数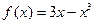
．
（Ⅰ）求函数
的图象在点
处的切线
的方程；
（Ⅱ）求函数区间
上的最值．
（本小题满分12分）
如图，长方体
中，
，
，
是
中点，
是
中点．
(Ⅰ)求证：
；
（Ⅱ）求证：平面
⊥平面
．
（本小题满分12分）
已知椭圆
的焦点为
，且过点
．
(Ⅰ) 求椭圆的标准方程；
（Ⅱ）设直线
交椭圆于
两点，求线段
的中点
坐标．
(本小题满分14分)
本题是选作题，考生只能选做其中两个小题．三个小题都作答的，以前两个小题计算得分。
①选修4－4《坐标系与参数方程》选做题（本小题满分7分）
已知曲线C的参数方程是
为参数)，且曲线C与直线
=0相交于两点A、B求弦AB的长。
②选修4－2《矩阵与变换》选做题（本小题满分7分）
已知矩阵
的一个特征值为
,它对应的一个特征向量
。
（Ⅰ）求矩阵M；
（Ⅱ）点P(1, 1)经过矩阵M所对应的变换,得到点Q，求点Q的坐标。
③选修4－5《不等式选讲》选做题（本小题满分7分）
函数
的图象恒过定点
,若点在直
线
上,其中
,求
的最小值。
(本小题满分14分)
已知函数
．
（1）讨论
函数
的单调性；
（2）当
为偶数时，正项数列
满足
，求的通项公式；
（3）当为奇数且
时，求证：
．