已知椭圆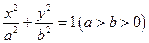 的离心率
的离心率 ,短轴长为
,短轴长为
(Ⅰ)求椭圆方程;
(Ⅱ)若椭圆与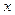 轴正半轴、
轴正半轴、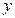 轴正半轴的交点分别为
轴正半轴的交点分别为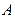 、
、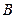 ,经过点
,经过点 且斜率k的直线
且斜率k的直线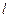 与椭圆交于不同的两点
与椭圆交于不同的两点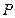 、
、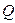 ,是否存在常数
,是否存在常数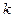 ,使得向量
,使得向量 共线?如果存在,求
共线?如果存在,求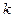 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。
已知抛物线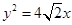 的焦点为椭圆
的焦点为椭圆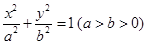 的右焦点,且椭圆的长轴长为4,M、N是椭圆上的的动点.
的右焦点,且椭圆的长轴长为4,M、N是椭圆上的的动点.
(1)求椭圆标准方程;
(2)设动点 满足:
满足: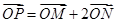 ,直线
,直线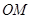 与
与 的斜率之积为
的斜率之积为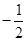 ,证明:存在定点
,证明:存在定点 使
使
得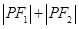 为定值,并求出
为定值,并求出 的坐标;
的坐标;
(3)若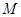 在第一象限,且点
在第一象限,且点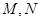 关于原点对称,
关于原点对称,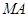 垂直于
垂直于 轴于点
轴于点 ,连接
,连接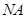 并延长交椭圆于点
并延长交椭圆于点 ,记直线
,记直线 的斜率分别为
的斜率分别为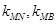 ,证明:
,证明: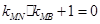 .
.
在四棱锥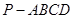 中,
中,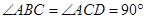 ,
,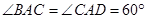 ,
,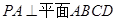 ,
,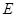 为
为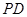 的中点,
的中点,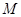 为
为 的中点,
的中点,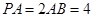 .
.
(1)求证: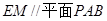 ;
;
(2)求证: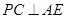 ;
;
(3)求三棱锥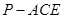 的体积
的体积 .
.
已知等差数列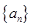 的前
的前 项和为
项和为 .
.
(1)请写出数列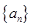 的前
的前 项和
项和 公式,并推导其公式;
公式,并推导其公式;
(2)若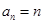 ,数列
,数列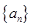 的前
的前 项和为
项和为 ,求
,求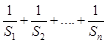 的和.
的和.
空气质量指数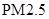 (单位:
(单位: )表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
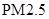 日均浓度 日均浓度 |
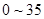 |
 |
 |
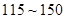 |
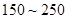 |
 |
| 空气质量级别 |
一级 |
二级 |
三级 |
四级 |
五级 |
六级 |
| 空气质量类别 |
优 |
良 |
轻度污染 |
中度污染 |
重度污染 |
严重污染 |
某市 年
年 月
月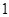 日—
日—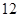 月
月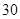 日(
日(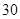 天)对空气质量指数
天)对空气质量指数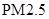 进行监测,获得数据后得到如下条形图.
进行监测,获得数据后得到如下条形图. 
(1)估计该城市一个月内空气质量类别为优的概率;
(2)从空气质量级别为三级和四级的数据中任取 个,求恰好有一天空气质量类别为中度污染的概率.
个,求恰好有一天空气质量类别为中度污染的概率.
设锐角三角形ABC的内角A,B,C的对边分别为 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,求
,求 的面积及
的面积及 .
.