(本小题满分12分)
某迷宫有三个通道,进入迷宫的每个人都要经过一扇智能门。首次到达此门,系统会随机(即等可能)为你打开一个通道,若是1号通道,则需要1小时走出迷宫;若是2号、3号通道,则分别需要2小时、3小时返回智能门。再次到达智能门时,系统会随机打开一个你未到过的通道,直至走完迷宫为止。令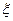 表示走出迷宫所需的时间。(1)求
表示走出迷宫所需的时间。(1)求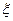 的分布列;(2)求
的分布列;(2)求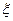 的数学期望。
的数学期望。
某村计划建造一个室内面积为800 的矩形蔬菜温室。在温室内,沿左、右两侧与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左、右两侧与后侧内墙各保留1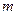 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3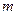 宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
从3名男生和2名女生中任选2人参加学校演讲比赛。
⑴求所选 2人恰有
2人恰有 名女生的概率;
名女生的概率;
⑵求所选2人中至少有 名
名 女生的概率.
女生的概率.
⑴在 中,已知
中,已知 求此三角形最小边的长;
求此三角形最小边的长; ⑵在
⑵在 中
中 ,已知
,已知 ,求
,求 .
.

随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图 .
⑴根据茎叶图判断哪个班的平均身高较高;
⑵计算甲班的样本方差.
(本小题满分14分:6+8)
某投资公司投资甲、乙两个项目所得的利润分别是 P(亿元)和Q(亿元),它们与投资额t(亿元)的关系有经验公式
P(亿元)和Q(亿元),它们与投资额t(亿元)的关系有经验公式 ,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所得的总利润为y(亿元)
,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所得的总利润为y(亿元)
(1)求y关于x的函数表达式;
(2)求总利润的最大值。