⑴在 中,已知
中,已知 求此三角形最小边的长;
求此三角形最小边的长; ⑵在
⑵在 中
中 ,已知
,已知 ,求
,求 .
.
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13, 14);第二组[14, 15),……,第五组[17, 18]. 下图是按上述分组方法得到的频率分布直方图.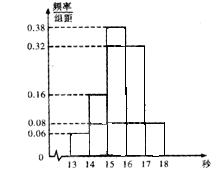
(1)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(2)设m、n表示该班某两位同学的百米测试成绩,且已知m, n∈[13, 14)∪[17, 18]. 求事件“|m-n|>1”的概率.
如图,正三角形ABC的边长为2,D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠,使A、B、C三点重合,构成三棱锥A— DEF.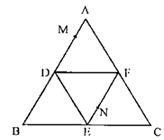
(I)求平面ADE与底面DEF所成二面角的余弦值
(Ⅱ)设点M、N分别在AD、EF上,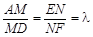 (λ>O,λ为变量)
(λ>O,λ为变量)
①当λ为何值时,MN为异面直线AD与EF的公垂线段? 请证明你的结论②设异面直线MN与AE所成的角为a,异面直线MN与DF所成的角为β,试求a+β 的值
如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点.
(1)求证:平面EBD⊥平面SAC;
(2)设SA=4,AB=2,求点A到平面SBD的距离;
如图,正三棱柱ABC—A1B1C1的底面边长的3,侧棱AA1=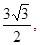 D是CB延长线上一点,且BD=BC.
D是CB延长线上一点,且BD=BC.
(Ⅰ)求证:直线BC1//平面AB1D;
(Ⅱ)求二面角B1—AD—B的大小;
(Ⅲ)求三棱锥C1—ABB1的体积.
下列五个正方体图形中,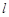 是正方体的一条对角线,点M,N,P分别为其所在棱的中点,求能得出
是正方体的一条对角线,点M,N,P分别为其所在棱的中点,求能得出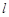 ⊥面MNP的图形的序号(写出所有符合要求的图形序号)
⊥面MNP的图形的序号(写出所有符合要求的图形序号)
