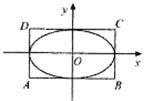
(本小题满分13分)如图,椭圆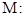
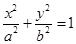 (
(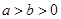 )的离心率为
)的离心率为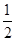 ,直线
,直线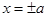 和
和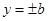 所围成的矩形
所围成的矩形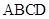 的面积为
的面积为 .
.
(Ⅰ)求椭圆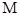 的标准方程;
的标准方程;
(Ⅱ)若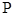 为椭圆
为椭圆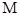 上任意一点,
上任意一点, 为坐标原点,
为坐标原点,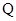 为线段
为线段 的中点,求点
的中点,求点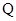 的轨迹方程;
的轨迹方程;
(Ⅲ)已知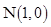 ,若过点
,若过点 的直线
的直线 交点
交点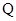 的轨迹于
的轨迹于 ,
,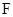 两点,且
两点,且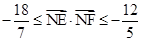 ,求直线
,求直线 的斜率的取值范围.
的斜率的取值范围.
已知a=(sin α,1), b=(cos α,2),α∈ .
.
(1)若a∥b,求tan α的值;
(2)若a·b= ,求sin
,求sin  的值.
的值.
已知函数f(x)=ax+x2,g(x)=xln a,a>1.
(1)求证:函数F(x)=f(x)-g(x)在(0,+∞)上单调递增;
(2)若函数y=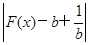 -3有四个零点,求b的取值范围;
-3有四个零点,求b的取值范围;
(3)若对于任意的x1,x2∈[-1,1]时,都有|F(x2)-F(x1)|≤e2-2恒成立,求a的取值范围.
已知函数f(x)=ln ax- (a≠0).
(a≠0).
(1)求函数f(x)的单调区间及最值;
(2)求证:对于任意正整数n,均有1+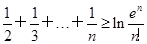 (e为自然对数的底数);
(e为自然对数的底数);
(3)当a=1时,是否存在过点(1,-1)的直线与函数y=f(x)的图象相切?若存在,有多少条?若不存在,请说明理由.
已知二次函数f(x)的二次项系数为a,且不等式f(x)>2x的解集为(-1,3).
(1)若函数g(x)=xf(x)在区间 内单调递减,求a的取值范围;
内单调递减,求a的取值范围;
(2)当a=-1时,证明方程f(x)=2x3-1仅有一个实数根;
(3)当x∈[0,1]时,试讨论|f(x)+(2a-1)x+3a+1|≤3成立的充要条件.
已知函数f(x)=aln(2x+1)+bx+1.
(1)若函数y=f(x)在x=1处取得极值,且曲线y=f(x)在点(0,f(0))处的切线与直线2x+y-3=0平行,求a的值;
(2)若b=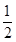 ,试讨论函数y=f(x)的单调性.
,试讨论函数y=f(x)的单调性.