（本小题满分12分）
已知函数
，且函数
的最小正周期
为
（1）若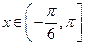
，求函数的单调递减区间；
（2）将函数
的图象上各点的纵坐标保持不变，横坐标缩短到原来的
，把所得到的图象再向左平移
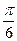个单位，得到函数
的图象，求函数在区间
上的最小值。
（本小题共9分）
已知函数f（x）=
。
（Ⅰ）求函数f（x）的定义域；
（Ⅱ）判断函数f（x）的奇偶性，并证明；
（Ⅲ）判断函数f（x）在定义域上的单调性，并用定义证明。
（本小题共9分）
已知集合A={x|2≤x≤8}，B={x|1<x<6}，C={x|x>a}，U=R
（Ⅰ）求A∪B，（C 
A）∩B；
（Ⅱ）若A∩C≠
，求a的取值范围。
已知
在点（1，f(1)）处的切线方程为
。
（1）求f(x)的表达式；
（2）若f(x)满足
恒成立，则称f(x)为g(x)的一个“上界函数”，如果f(x)为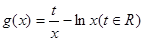
的一个“上界函数”，求t的取值范围；
（3）当m>0时讨论
在区间（0，2）上极值点的个数。
设Sn为数列{an}为前n项和，对任意的
都有
（m为常数且m>0）
（1）求证：{an}为等比数列；
（2）设数列{an}的公比q=f(m)，数列{bn}满足
，求数列{bn}的通项公式；
（3）在（2）的条件下，求数列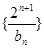
的前n项和Tn。
已知函数f(x)和g(x)的图象关于原点对称，且
（1）求函数g(x)的解析式；
（2）解不等式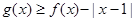
；
（3）若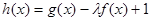
在[－1，1]上是增函数，求实数
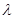的取值范围。