(本小题满分12分)
已知在四棱锥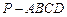 中,底面
中,底面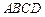 是边长为4的正方形,平面
是边长为4的正方形,平面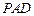 ⊥平面
⊥平面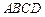 ,△
,△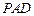 是正三角形,
是正三角形, 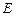 、
、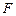 、
、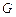 分别是
分别是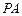 、
、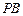 、
、 的中点.
的中点.
(I)求证: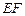
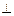 平面
平面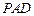 ;
;
(II)求平面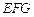 与平面
与平面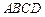 所成锐二面角的大小.
所成锐二面角的大小.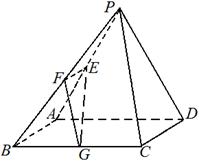
(本小题满分12分)在 中,
中, ,
, .
. 求角
求角 的值;
的值; 设
设 ,求
,求 .
.
(本小题满分14分)
已知函数 (其中
(其中 ,e是自然对数的底数,e=2.71828…).
,e是自然对数的底数,e=2.71828…).
(Ⅰ)当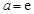 时,求函数
时,求函数 的极值;
的极值;
(Ⅱ)若 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(Ⅲ)求证:对任意正整数n,都有 .
.
(本小题满分13分)
已知椭圆Ω: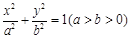 的焦距为
的焦距为 ,且经过点
,且经过点 .
.
(Ⅰ)求椭圆Ω的方程;
(Ⅱ)A是椭圆Ω与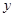 轴正半轴的交点, 椭圆Ω上是否存在两点M、N,使得△AMN是以A为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
轴正半轴的交点, 椭圆Ω上是否存在两点M、N,使得△AMN是以A为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
(本小题满分12分)
等差数列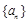 的前n项和为
的前n项和为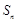 ,数列
,数列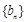 是等比数列,满足
是等比数列,满足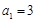 ,
,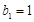 ,
,  ,
,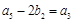 .
.
(Ⅰ)求数列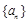 和
和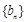 的通项公式;
的通项公式;
(Ⅱ)令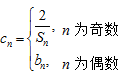 设数列
设数列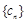 的前n项和
的前n项和 ,求
,求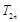 .
.
(本小题满分12分)
四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N分别是AB、SC的中点.
(Ⅰ)求证:MN∥平面SAD;
(Ⅱ)求二面角S-CM-D的余弦值.