(本小题满分12分)
四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N分别是AB、SC的中点.
(Ⅰ)求证:MN∥平面SAD;
(Ⅱ)求二面角S-CM-D的余弦值.
先后2次抛掷一枚质地均匀的骰子,将得到的点数分别记为a,b.
(1) 求a+b=7的概率;
(2) 求直线ax+by+5=0与圆 = 1相切的概率。
设数列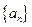 的前
的前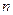 项和为
项和为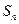 ,已知
,已知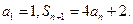
(1)设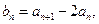 证明数列
证明数列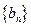 是等比数列;
是等比数列;
(2)求数列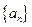 的通项公式;
的通项公式;
(3)求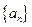 的前
的前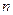 项和
项和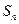 .
.
已知直线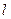 过点
过点 ,圆
,圆 :
: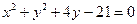 .
.
(1)求截得圆 弦长最长时
弦长最长时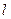 的直线方程;
的直线方程;
(2)若直线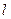 被圆N所截得的弦长为
被圆N所截得的弦长为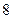 ,求直线
,求直线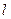 的方程.
的方程.
如图,在河的对岸可以看到两个目标物M,N,但不能到达,在河岸边选取相距40米的两个目标物P,Q两点,测得 ,
, ,
,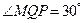 ,
, ,试求两个目标物M,N之间的距离.
,试求两个目标物M,N之间的距离.
(满分12分)
如图,在正方体 中,E、F、G分别为
中,E、F、G分别为 、
、 、
、 的中点,O为
的中点,O为 与
与 的交点,
的交点,
(1)证明: 面
面
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.