设数列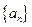 的前
的前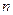 项和为
项和为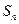 ,已知
,已知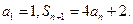
(1)设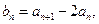 证明数列
证明数列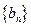 是等比数列;
是等比数列;
(2)求数列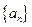 的通项公式;
的通项公式;
(3)求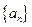 的前
的前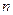 项和
项和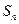 .
.
(本小题满分12分)
在平面直角坐标系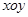 中,已知三点
中,已知三点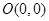 ,
,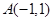 ,
, ,曲线C上任意—点
,曲线C上任意—点 满足:
满足: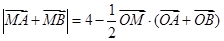 .
.
(l)求曲线C的方程;
(2)设点P是曲线C上的任意一点,过原点的直线L与曲线相交于M,N两点,若直线PM,PN的斜率都存在,并记为 ,
, .试探究
.试探究 的值是否与点P及直线L有关,并证明你的结论;
的值是否与点P及直线L有关,并证明你的结论;
(3)设曲线C与y轴交于D、E两点,点M (0,m)在线段DE上,点P在曲线C上运动.若当点P的坐标为(0,2)时, 取得最小值,求实数m的取值范围.
取得最小值,求实数m的取值范围.
如图,a是海面上一条南北方向的海防警戒线,在a上一点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20km和54km处。某时刻,监测点B收到发自静止目标P的一个声波,8s后监测点A、20s后监测点C相继收到这一信号。在当时的气象条件下,声波在水中传播速度是 .
.
(1)设A到P的距离为xkm,用x表示B,C到P的距离,并求x的值;
(2)求静止目标P到海防警戒线a的距离。
(本小题满分12分)
已知平面区域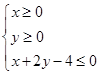 被圆C及其内部所覆盖.
被圆C及其内部所覆盖.
(1)当圆C的面积最小时,求圆C的方程;
(2)若斜率为1的直线l与(1)中的圆C交于不同的两点A、B,且满足CA⊥CB,求直线l的方程.
(本小题满分10分)
已知集合
(1)若 求实数m的值;
求实数m的值;
(2)设集合为R,若 ,求实数m的取值范围。
,求实数m的取值范围。
(本小题满分12分)
已知椭圆 的中心在坐标原点、对称轴为坐标轴,且抛物线
的中心在坐标原点、对称轴为坐标轴,且抛物线 的焦点是它的一个焦点,又点
的焦点是它的一个焦点,又点 在该椭圆上.
在该椭圆上.
(1)求椭圆 的方程;
的方程;
(2)若斜率为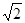 直线
直线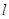 与椭圆
与椭圆 交于不同的两点
交于不同的两点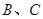 ,当
,当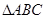 面积的最大值时,求直线
面积的最大值时,求直线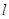 的方程.
的方程.