让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系。
第一步:数轴上两点连线的中点表示的数
自己画一个数轴,如果点A、B分别表示-2、4,则线段AB的中点M表示的数是 。 再试几个,我们发现:
数轴上连结两点的线段的中点所表示的数是这两点所表示数的平均数。
第二步;平面直角坐标系中两点连线的中点的坐标(如图①)
为便于探索,我们在第一象限内取两点A(x1,y1),B(x2,y2),取线段AB的中点M,分别作A、B到x轴的垂线段AE、BF,取EF的中点N,则MN是梯形AEFB的中位线,故MN⊥x轴,利用第一步的结论及梯形中位线的性质,我们可以得到点M的坐标是( , )(用x1,y1,x2,y2表示),AEFB是矩形时也可以。我们的结论是:平面直角坐标系中连结两点的线段的中点的横(纵)坐标等于这两点的横(纵)坐标的平均数。
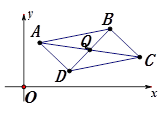
图① 图②
第三步:平面直角坐标系中平行四边形的顶点坐标之间的关系(如图②)
在平面直角坐标系中画一个平行四边形ABCD,设A(x1,y1),B(x2,y2),C(x3,y3),
D(x4,y4),则其对角线交点Q的坐标可以表示为Q( , ),也可以表示为Q( , ),经过比较,我们可以分别得出关于x1,x2,x3,x4及,y1,y2,y3,y4的两个等式是 和 。 我们的结论是:平面直角坐标系中平行四边形的对角顶点的横(纵)坐标的 。
解方程组或不等式组
(1)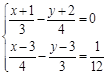 (2)
(2)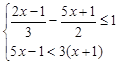
如图,某化工厂与A,B两地有公路和铁路相连,这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5元/(吨•千米),铁路运价为1.2元/(吨•千米),这两次运输共支出公路运费15 000元,铁路运费97 200元,请计算这批产品的销售款比原料费和运输费的和多多少元?
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
甲:
乙:
根据甲,乙两名同学所列方程组,请你分别指出未知数x,y表示的意义,然后在等式右边的方框内补全甲、乙两名同学所列方程组.
甲:x表示 ,y表示
乙:x表示 ,y表示
(2)甲同学根据他所列方程组解得x=300,请你帮他解出y的值,并解决该实际问题.
如图,AD=CD,AC平分∠DAB,求证:DC∥AB.
小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.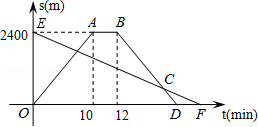
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.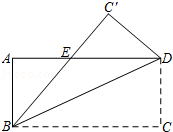
(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求△BDE的面积.