(本小题满分12分已知二次函数f(x) 对任意x∈R,都有f (1-x)="f" (1+x)成立,设向量a="(sinx,2)," b=(2sinx,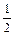 ),
),
c=(cos2x,1),d=(1,2)。
(1)分别求a·b和c·d的取值范围;
(2)当x∈[0,π]时,求不等式f(a·b)>f(c·d)的解集.
(本小题满分12分)
已知椭圆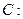
 的离心率为
的离心率为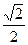 ,点
,点 是椭圆上的一点,且点
是椭圆上的一点,且点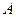 到椭圆
到椭圆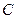 的两焦点的距离之和为4,
的两焦点的距离之和为4,
(1)求椭圆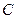 的方程;
的方程;
(2)过点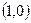 作直线
作直线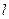 与椭圆
与椭圆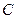 交于
交于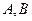 两点,
两点,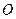 是坐标原点,设
是坐标原点,设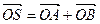 ,是否存在这样的直线
,是否存在这样的直线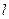 ,使四边形
,使四边形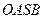 的对角线长相等?若存在,求出
的对角线长相等?若存在,求出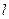 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。
(本小题满分12分)
已知函数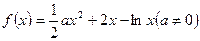
(1)当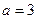 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)若 存在单调增区间,求
存在单调增区间,求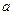 的取值范围。
的取值范围。
(本小题满分12分)
命题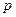 :方程
:方程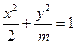 是焦点在
是焦点在 轴上的椭圆,
轴上的椭圆,
命题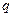 :函数
:函数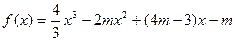 在
在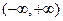 上单调递增,
上单调递增,
若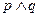 为假,
为假,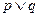 为真,求实数
为真,求实数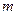 的取值范围.
的取值范围.
(本小题满分10分)
设命题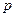 :
: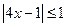 ;命题
;命题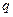 :
: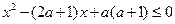 .
.
若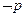 是
是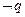 的必要不充分条件,求实数
的必要不充分条件,求实数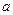 的取值范围.
的取值范围.
已知抛物线方程为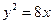 ,
,
(1)直线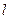 过抛物线的焦点
过抛物线的焦点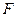 ,且垂直于
,且垂直于 轴,
轴,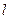 与抛物线交于
与抛物线交于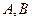 两点,求
两点,求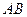 的长度。
的长度。
(2)直线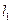 过抛物线的焦点
过抛物线的焦点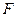 ,且倾斜角为
,且倾斜角为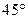 ,直线
,直线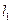 与抛物线相交于
与抛物线相交于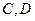 两点,
两点,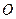 为原点。求△
为原点。求△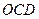 的面积。
的面积。