（本小题满分13分）
已知抛物线
的顶点在原点，焦点为
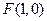，且过点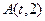
.
（1）求t的值；
（2）若直线
与抛物线只有一个公共点，求实数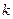
的值.
如图，四棱锥P—ABCD中，底面四边形ABCD是正方形，侧面PDC是边长为a的正
三角形，且平面PDC⊥底面ABCD，E为PC的中点。
|
（I）求异面直线PA与DE所成的角；
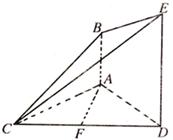
（II）求点D到面PAB的距离.如图，直二面角D—AB—E中，四边形ABCD是边长为2的正方形，AE=EB，F
为CE上的点，且BF⊥平面ACE.
（Ⅰ）求证：AE⊥平面BCE；
（Ⅱ）求二面角B—AC—E的余弦值；
（Ⅲ）求点D到平面ACE的距离.
已知
，
为
上的点.
（1）当
；
（2）当二面角—
—
的大小为
的值.
如图，在五面体，ABCDF中，点O是矩形ABCD的对角线的交点，面ABF是等边三角形，棱EF＝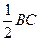
．
（1）证明EO∥平面ABF；
（2）问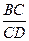
为何值时，有OF⊥ABE，试证明你的结论．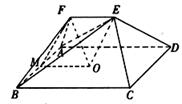
如图，已知AB⊥平面ACD，DE//AB，△ACD是正三角形，AD=DE=2AB，且F
是CD的中点。
（I）求证：AF//平面BCE；
（II）求证：平面BCE⊥平面CDE；
（III）求平面BCE与平面ACD所成锐二面角的大小。
