已知 ,
, 为
为 上的点.
上的点.
(1)当 ;
;
(2)当二面角 —
— —
— 的大小为
的大小为 的值.
的值.
(本小题满分14分)
已知函数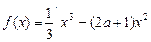
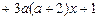 ,a∈R.
,a∈R.
(1)当a=0时,求曲线y=f(x)在点(3,f(3))处的切线方程:
(2)当函数y=f'(x)在(0,4)上有唯一的零点时,求实数a的取值范围.
(本小题满分14分)已知△ABC三个内角A、B、C的对边为a、b、c,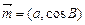 ,
, ,a≠b,已知
,a≠b,已知 .
.
(1)判断三角形的形状,并说明理由。
(2)若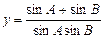 ,试确定实数y的取值范围.
,试确定实数y的取值范围.
(本小题满分12分)
已知向量


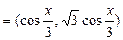 ,函数
,函数
 ·
· ,
,
(1)求函数f(x)的单调递增区间;
(2)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函
数f(x)的值域.
(本小题满分12分)已知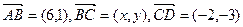 ,
,
(1)若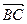 //
//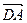
 ,求
,求 与
与 之间的关系式;
之间的关系式;
(2)在(1)的前提下,若 ,求向量
,求向量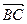 的模的大小。
的模的大小。
(本小题满分12分)
已知椭圆的中心在坐标原点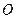 ,焦点在
,焦点在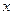 轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.
轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线 过
过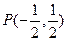 且与椭圆相交于A,B两点,当P是AB的中点时,
且与椭圆相交于A,B两点,当P是AB的中点时,
求直线 的方程.
的方程.