某少数民族的刺绣有着悠久的历史，如下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案，这些图案都是由小正方形构成，小正方形数越多刺绣越漂亮．现按同样的规律刺绣(小正方形的摆放规律相同)，设第
个图形包含
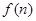个小正方形．
(1)求出
的值；
(2)利用合情推理的“归纳推理思想”，归纳出
与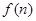之间的关系式，并根据你得到的关系式求出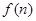的表达式；
(3)求
的值.
某中学高三年级从甲（文）、乙（理）两个年级组各选出7名学生参加高校自主招生数学选拔考试，他们取得的成绩（满分100分）的茎叶图如图所示，其中甲组学生的平均分是85，乙组学生成绩的中位数是83．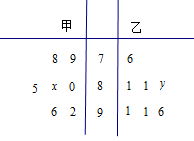
（1）求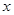
和
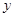的值；
（2）计算甲组7位学生成绩的方差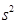
；
（3）从成绩在90分以上的学生中随机抽取两名学生，求甲组至少有一名学生的概率．
已知函数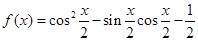
（1）求函数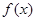
的最小正周期和值域；
（2）若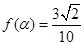
，求
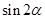的值．
已知函数
.
（1）求函数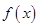
的单调区间；
（2）若
，设
，
是函数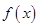图像上的任意两点（
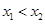），记直线AB的斜率为
，求证：
.
已知双曲线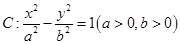
，
分别是它的左、右焦点，
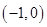是其左顶点，且双曲线的离心率为
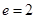.设过右焦点
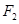的直线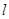
与双曲线C的右支交于
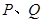两点，其中点位于第一象限内.
（1）求双曲线的方程；
（2）若直线
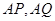分别与直线
交于
两点，求证：
；
（3）是否存在常数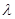
，使得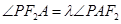
恒成立？若存在，求出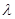的值，若不存在，请说明理由。
已知数列
满足
，
，
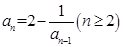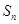是数列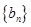
的前n项和，且有
.
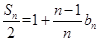（1）证明：数列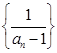
为等差数列；（2）求数列
的通项公式；
（3）设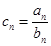
，记数列
的前n项和
，求证：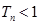
.