(本题满分14分) 某中学为了解学生的睡眠情况与学习效率的关系，从中抽取20名学生作为样本进行调查.调查的数据整理分组如下表示：
| 睡眠时间（单位：小时） |
 |
 |
 |
 |
 |
 |
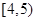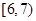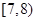| 频 数 |
1 |
3 |
|
6 |
4 |
|
| 频 率 |
|
|
0．20 |
|
|
|
（1）将以上表格补充完整，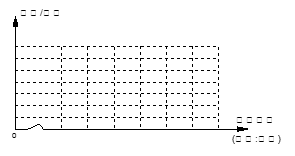
（2）在给定的坐标系内画出样本的频率分布直方图；
（3）为了比较睡眠情况与学习效率的关系，现从睡眠时间在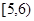
与个小时的学生中抽取2人，问能在这两个睡眠时间内各抽到1个学生的概率是多少？
（
，
为常数），且方程
有两个实根为
.
的解析式；
是定义在
上的减函数，并且满足
，
,
,
的值，（2）如果
，求x的取值范围。
,
，集合B=
。
=2时，求
； 
时，若元素
是
的必要条件，求实数
中，底面
为矩形，侧面
底面
，
，
．
；
与平面
所成的角为
， 
的余弦值．