.如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD= .
.
(1)求四棱锥S-ABCD的体积;
(2)求证:面SAB⊥面SBC;
(3)求二面角 的正切值.
的正切值.
(本小题满分12分)某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产100件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为500件,产品销售数量为t件时,销售所得的收入为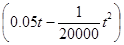 万元.
万元.
(1)该公司这种产品的年生产量为x件,生产并销售这种产品所得到的利润关于当年产量x的函数为f(x),求f(x);
(2)当该公司的年产量为多少件时,当年所获得的利润最大?
(本小题满分12分)已知向量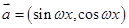 ,
,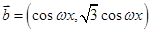
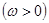 函数
函数 的最小正周期为
的最小正周期为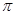 .
.
(1)求函数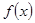 的单调增区间;
的单调增区间;
(2)如果△ABC的三边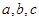 所对的角分别为
所对的角分别为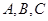 ,且满足
,且满足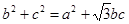 求
求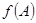 的值.
的值.
(本小题满分12分)已知命题 :
: ,命题
,命题 :
: ,若“
,若“ 且
且 ”为真命题,求实数a的取值范围.
”为真命题,求实数a的取值范围.
(本小题满分12分)已知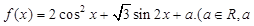 为常数)
为常数)
(1)若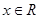 ,求
,求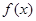 的最小正周期;
的最小正周期;
(2)若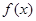 在[
在[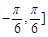 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求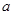 的值.
的值.
已知函数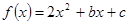 在
在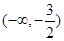 上是减函数,在
上是减函数,在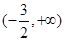 上是增函数,且对应方程两个实根
上是增函数,且对应方程两个实根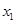 ,
,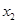 满足
满足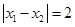 ,
,
(1)求二次函数的解析式;
(2)求函数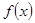 在区间
在区间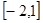 上的值域
上的值域