(本题14分)数列
的前
项和为
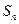，已知
（1）证明：数列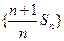
是等差数列，并求；
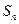（2）设
，求证：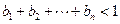
.
如图，在四棱锥P‐ABCD中，四边形ABCD为正方形，PA⊥平面ABCD，E为PD的中点．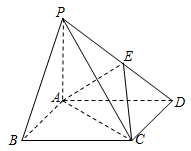
求证：（1）PB∥平面AEC；（2）平面PCD⊥平面PAD．
（本小题满分14分）已知直线
和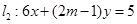
.
问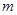
为何值时，有：（1）
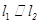？（2）
？
已知半径为5的圆的圆心在
轴上，圆心的横坐标是整数，且与直线
相切．
（1）求圆的标准方程；
（2）设直线
与圆相交于
两点，求实数
的取值范围；
（3）在（2）的条件下，是否存在实数
，使得弦
的垂直平分线
过点
.
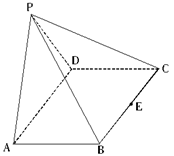
（本小题16分）四棱锥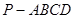
中，底面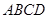
是边长为8的菱形，
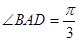，若
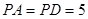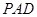，平面
⊥平面.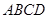
（1）求四棱锥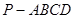的体积；
（2）求证：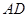
⊥
.
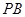已知圆心
（Ⅰ）写出圆C的标准方程；
（Ⅱ）过点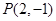
作圆C的切线，求切线的方程及切线的长.