学完“等腰三角形”一章后,老师布置了一道思考题:如图,点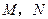 分别在正△
分别在正△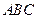 的
的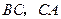 边上,且
边上,且 ,
,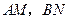 交于点
交于点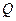 .
.
求证:
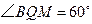 .
.做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“ ”与“
”与“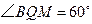 ”的位置交换,得到的是否仍是真命题?
”的位置交换,得到的是否仍是真命题?
②若将题中的点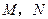 分别移动到
分别移动到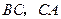 的延长线上,是否仍能得到
的延长线上,是否仍能得到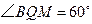 ?
?
③若将题中的条件“点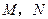 分别在正三角形
分别在正三角形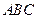 的
的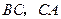 边上”改为“点
边上”改为“点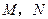 分别在正方形
分别在正方形 的
的 边上”,是否仍能得到
边上”,是否仍能得到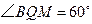 ?……
?……
请你作出判断,是的填“是”,否的算出度数填在横线上,① ;② ;③ .画图并证明 ②.
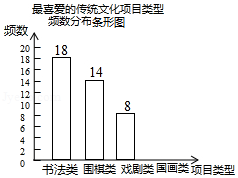
某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
最喜爱的传统文化项目类型频数分布表
|
项目类型 |
频数 |
频率 |
|
书法类 |
18 |
|
|
围棋类 |
14 |
0.28 |
|
喜剧类 |
8 |
0.16 |
|
国画类 |
|
0.20 |
根据以上信息完成下列问题:
(1)直接写出频数分布表中 的值;
(2)补全频数分布条形图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
在一只不透明的袋子中装有2个白球和2个黑球,这些球除颜色外都相同.
(1)若先从袋子中拿走 个白球,这时从袋子中随机摸出一个球是黑球的事件为“必然事件”,则 的值为 ;
(2)若将袋子中的球搅匀后随机摸出1个球(不放回),再从袋中余下的3个球中随机摸出1个球,求两次摸到的球颜色相同的概率.
某校对七、八、九年级的学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等级.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
|
各年级学生成绩统计表 |
||||
|
优秀 |
良好 |
合格 |
不合格 |
|
|
七年级 |
|
20 |
24 |
8 |
|
八年级 |
29 |
13 |
13 |
5 |
|
九年级 |
24 |
|
14 |
7 |
根据以上信息解决下列问题:
(1)在统计表中, 的值为 , 的值为 ;
(2)在扇形统计图中,八年级所对应的扇形圆心角为 度;
(3)若该校三个年级共有2000名学生参加考试,试估计该校学生体育成绩不合格的人数.
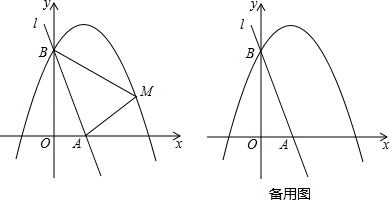
如图,直线 与 轴、 轴分别相交于 、 两点,抛物线 经过点 .
(1)求该抛物线的函数表达式;
(2)已知点 是抛物线上的一个动点,并且点 在第一象限内,连接 、 ,设点 的横坐标为 , 的面积为 ,求 与 的函数表达式,并求出 的最大值;
(3)在(2)的条件下,当 取得最大值时,动点 相应的位置记为点 .
①写出点 的坐标;
②将直线 绕点 按顺时针方向旋转得到直线 ,当直线 与直线 重合时停止旋转,在旋转过程中,直线 与线段 交于点 ,设点 、 到直线 的距离分别为 、 ,当 最大时,求直线 旋转的角度(即 的度数).
不透明袋子里装有红色、绿色小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,求两次都摸到红色小球的概率.