如图,平面 平面
平面 ,
, 是正方形,
是正方形, ,且
,且 ,
, 、
、 、
、 分别是线段
分别是线段 、
、 、
、 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求异面直线 、
、 所成角的余弦值.
所成角的余弦值.
在某次高三考试成绩中,随机抽取了9位同学的数学成绩进行统计。下表是9位同学的选择题和填空题的得分情况(选择题满分60分,填空题满分16分):
| 选择题 |
40 |
55 |
50 |
45 |
50 |
40 |
45 |
60 |
40 |
| 填空题 |
12 |
16 |
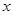 |
12 |
16 |
12 |
8 |
12 |
8 |
(Ⅰ)若这9位同学填空题得分的平均分为12分,试求表中的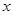 的值及他们填空题得分的标准差;
的值及他们填空题得分的标准差;
(Ⅱ)在(1)的条件下,记这9位同学的选择题得分组成的集合为A,填空题得分组成的集合为B。若同学甲的解答题的得分是46分,现分别从集合A、B中各任取一个值当作其选择题和填空题的得分,求甲的数学成绩高于100分的概率。
已知等差数列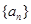 的前
的前 项和为
项和为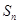 ,公差
,公差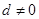 ,且
,且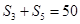 ,
,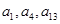 成等比数列.
成等比数列.
(1)求数列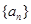 的通项公式;
的通项公式;
(2)设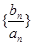 是首项为1公比为3 的等比数列,求数列
是首项为1公比为3 的等比数列,求数列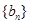 前
前 项和
项和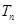 .
.
已知函数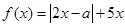 ,其中实数
,其中实数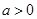 .
.
(1)当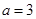 时,求不等式
时,求不等式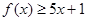 的解集;
的解集;
(2)若不等式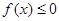 的解集为
的解集为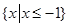 ,求
,求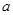 的值.
的值.
在直角坐标系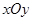 中,曲线
中,曲线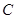 的参数方程为
的参数方程为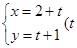 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点 为极点,
为极点,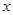 轴的正半轴为极轴的极坐标系下,曲线
轴的正半轴为极轴的极坐标系下,曲线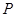 的方程为
的方程为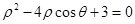 .
.
(1)求曲线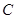 的普通方程和曲线
的普通方程和曲线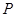 的直角坐标方程;
的直角坐标方程;
(2)设曲线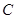 和曲线
和曲线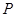 的交点
的交点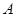 、
、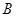 ,求
,求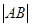 .
.