如图,平面 平面
平面 ,
, 是正方形,
是正方形, ,且
,且 ,
, 、
、 、
、 分别是线段
分别是线段 、
、 、
、 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求异面直线 、
、 所成角的余弦值.
所成角的余弦值.
已知圆 及定点
及定点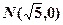 ,点
,点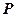 是圆
是圆 上的动点,
上的动点,
点 在
在 上,点
上,点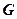 在
在 上,且满足
上,且满足 ,
, .
.
(1)求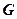 的轨迹
的轨迹 的方程;
的方程;
(2)过点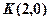 作直线
作直线 ,与曲线
,与曲线 交于
交于 两点,
两点, 为坐标原点,设
为坐标原点,设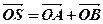 ,是否存在这样的直线
,是否存在这样的直线 ,使四边形
,使四边形 的对角线相等?若存在,求出直线
的对角线相等?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知直线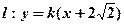 与圆
与圆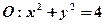 相交于
相交于 两点,
两点,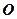 为坐标原点,
为坐标原点, 的面积为
的面积为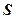 .
.
(1)试将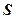 表示成
表示成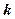 的函数
的函数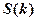 ,并求出其定义域;
,并求出其定义域;
(2)求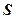 的最大值,并求取得最大时
的最大值,并求取得最大时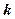 的值.
的值.
如图,已知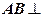 平面
平面 ,
, 平面
平面 ,
,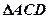 为等边三角形,
为等边三角形,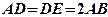 ,
,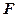 为
为 中点.
中点.
(1)求证: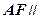 平面
平面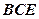 ;
;
(2)求证:平面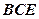
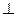 平面
平面 ;
;
(3)求直线 与平面
与平面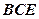 所成角的正弦值.
所成角的正弦值.
已知向量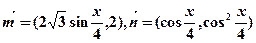 .
.
(1)若 ,求
,求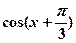 的值;
的值;
(2)记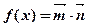 ,在
,在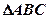 中,角
中,角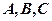 的对边分别为
的对边分别为 ,且满足
,且满足 ,求
,求 的取值范围.
的取值范围.
已知数列 是首项为1的等差数列,且
是首项为1的等差数列,且 ,若
,若 成等比数列,(1)求数列
成等比数列,(1)求数列 的通项公式;(2)设
的通项公式;(2)设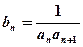 ,求数列
,求数列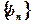 的前
的前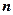 项和
项和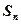 .
.