在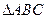 中,
中,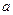 、
、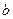 、
、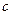 分别是角
分别是角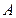 、
、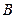 、
、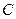 的对边,
的对边,
且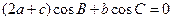 .
.
(Ⅰ)求角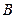 的值;
的值;
(Ⅱ)已知函数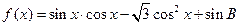 ,求
,求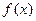 的单调递增区间
的单调递增区间
在抽样方法中,有放回抽样与无放回抽样中个体被抽到的概率是不同的,但当总体的容量很大而抽取的样本容量很小时,无放回抽样可以近似看作有放回抽样。现有一大批产品,采用随机抽样的方法一件一件抽取进行检验。若抽查的4件产品中未发现不合格产品,则停止检查,并认为该批产品合格;若在查到第4件或在此之前发现不合格产品,则也停止检查,并认为该批产品不合格。假定该批产品的不合格率为0.1,设检查产品的件数为X。
(Ⅰ)求随机变量X的分布列和数学期望;
(Ⅱ)通过上述随机抽样的方法进行质量检查,求认为该批产品不合格的概率
正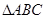 的边长为4,CD是AB边上的高,E、F分别是AC和BC的中点(如图(1)).现将
的边长为4,CD是AB边上的高,E、F分别是AC和BC的中点(如图(1)).现将 沿CD翻折成直二面角A-DC-B(如图(2)).
沿CD翻折成直二面角A-DC-B(如图(2)).
在图形(2)中:
(Ⅰ)试判断直线AB与平面DEF的位置关系,并说明理由;
(Ⅱ)求二面角E-DF-C的余弦值;
(Ⅲ)在线段BC上是否存在一点P,使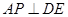 ?证明你的结论.
?证明你的结论.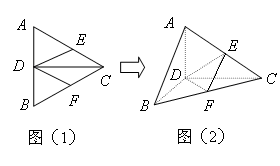
如图,港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问此时轮船离港口A还有多远?
已知函数
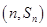 (
(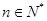 )均在函数
)均在函数 的图象上。
的图象上。
(Ⅰ)求数列 的通项公式
的通项公式 ;
;
(Ⅱ)令 证明:
证明: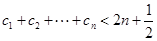
(本小题满分14分)已知函数 ,
,
(1)求函数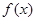 的单调区间,并判断是否有极值;
的单调区间,并判断是否有极值;
(2)若对任意的 ,恒有
,恒有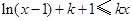 成立,求
成立,求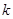 的取值范围;
的取值范围;
(3)证明: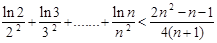 (
( ).
).