如图所示,横截面半径为r的圆柱体固定在水平地面上。一个质量为m的小滑块P从截面最高点A处以 滑下。不计任何摩擦阻力。
滑下。不计任何摩擦阻力。
(1)试对小滑块P从离开A点至落地的运动过程做出定性分析;
(2)计算小滑块P离开圆柱面时的瞬时速率和落地时的瞬时速率。
如图所示的直角坐标系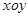 中,在
中,在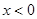 ,
,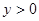 的区域有一对平行金属板M和N,其中N板位于
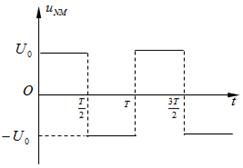
的区域有一对平行金属板M和N,其中N板位于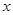 轴上,M、N板加有如图所示电压,平行金属板右侧存在沿y轴负向与平行金属板等宽度的匀强电场,场强大小为E,在
轴上,M、N板加有如图所示电压,平行金属板右侧存在沿y轴负向与平行金属板等宽度的匀强电场,场强大小为E,在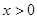
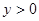 的区域存在垂直纸面的矩形有界磁场,其下边界和左边界分别与
的区域存在垂直纸面的矩形有界磁场,其下边界和左边界分别与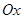 、
、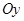 轴重合。
轴重合。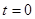 时刻一质量为
时刻一质量为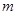 ,电量为
,电量为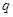 的带电微粒沿着平金属板的轴线
的带电微粒沿着平金属板的轴线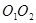 以初速度
以初速度 向右开始运动,恰从M板右边缘的P点沿
向右开始运动,恰从M板右边缘的P点沿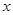 轴正向进入平行金属板右侧电场,经过一段时间后以
轴正向进入平行金属板右侧电场,经过一段时间后以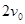 的速度经Q点进入磁场,Q点为
的速度经Q点进入磁场,Q点为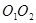 与y轴的交点,再经磁场偏转带电微粒恰好从坐标原点
与y轴的交点,再经磁场偏转带电微粒恰好从坐标原点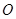 沿
沿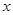 轴负向返回电场,不计带电微粒的重力。求:
轴负向返回电场,不计带电微粒的重力。求:
(1)平行金属板M、N间的距离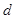 及右侧电场的宽度
及右侧电场的宽度 ;
;
(2)平行金属板上所加电压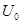 满足的条件;
满足的条件;
(3)矩形磁场区域的最小面积。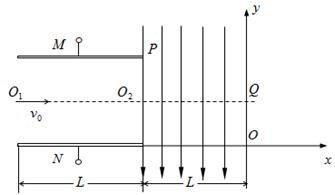
2012年4月30日4时50分,我国在西昌卫星发射中心用“长征三号乙”运载火箭首次采用“一箭双星”的方式,成功发射两颗北斗导航卫星,卫星顺利进入预定转移轨道。北斗卫星导航系统是中国自行研制开发的区域性有源三维卫星定位与通信系统(CNSS),其空间端包括5颗静止轨道卫星和30颗非静止轨道卫星,如图甲所示。
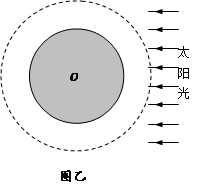
为简便起见,认为其中一颗卫星轨道平面与地球赤道平面重合,绕地心做匀速圆周运动(如图乙所示),与地心的距离为地球半径R0的2倍,卫星上的太阳能收集板可以把光能转化为电能,太阳能收集板的面积为S,在阳光下照射下每单位面积提供的最大电功率为P。已知地球表面重力加速度为g,近似认为太阳光是平行光,试估算:
(1)卫星做匀速圆周运动的周期;
(2)卫星绕地球一周,太阳能收集板工作时间及太阳能收集板最多可以转化多少电能?
2010年广州亚运盛会堪称是LED绿色照明技术、节能照明产品得到全面应用的照明科技博览会。无论是海心沙、广州塔、广州中轴线城市景观照明等重点工程项目,还是亚运城、大学城等数十个场馆和设施,处处都闪耀着国产LED绿色照明、节能照明产品的光芒。某实验小组要精确测定额定电压为3V的LED灯正常工作时的电阻,已知该灯正常工作时电阻大约500Ω左右,电学符号与小灯泡电学符号相同。
实验室提供的器材有:
额定电压为3V的LED灯,正常工作时电阻大约500Ω左右
电流表A2(量程为0至3mA,内阻RA2=15Ω)
定值电阻R2=1985Ω
滑动变阻器R1(0至20Ω)一只
电压表V(量程为0至12V,内阻RV=1kΩ)
蓄电池E(电动势为12V,内阻很小)
电键S一只
(1)不增减上述器材的情况下在下边方框中画出应采用的电路图
(2)写出测量LED灯正常工作时的电阻表达式Rx ,当表达式中的(填字母)达到,记下另一电表的读数代入表达式,其结果为正常工作时电阻。
如图所示,水平金属导轨MN、PQ固定于同一竖直平面上,高度差为3L,左端与水平放置的平行极板相连接,长方形区域Ⅰ、区域Ⅱ存在垂直导轨平面的匀强磁场,两磁场区域的宽度分别为L、2L,Ⅱ区磁感应强度大小是Ⅰ区的3倍. 金属杆CD在外力作用下能保持竖直状态,紧贴导轨匀速滑行,且与导轨接触良好. 当CD杆以2v0的速度水平向右进入Ⅰ区的磁场时,两极板中有一质量为m的带电油滴恰能平衡. 现让CD杆以v0的速度匀速通过两个磁场区域,杆刚进入Ⅰ区的磁场时,释放油滴,如果只考虑CD杆在两磁场区的过程,设油滴不会落到极板上,重力加速度为g. 求全过程:
(1)油滴能达到的最大速度vm;(2)电场力对油滴做的功W.
如图所示,半径为R的 1/4光滑圆弧轨道最低点D与水平面相切,在D点右侧L0=4R处用长为R的细绳将质量为m的小球B(可视为质点)悬挂于O点,小球B的下端恰好与水平面接触,质量为m的小球A(可视为质点)自圆弧轨道C的正上方H高处由静止释放,恰好从圆弧轨道的C点切入圆弧轨道,已知小球A与水平面间的动摩擦因数μ=0.5,细绳的最大张力Fm=7mg,重力加速度为g,试求: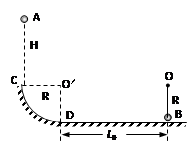
(1)若H=R,小球A到达圆弧轨道最低点D时所受轨道的支持力;
(2)试讨论H在什么范围内,小球A与B发生弹性碰撞后细绳始终处于拉直状态。