已知抛物线 ,焦点为F,顶点为O,点P在抛物线上移动,Q是OP的中点,M是FQ的中点,求点M的轨迹方程.
,焦点为F,顶点为O,点P在抛物线上移动,Q是OP的中点,M是FQ的中点,求点M的轨迹方程.
某鱼类养殖户在一个鱼池中养殖一种鱼,每季养殖成本为 元,此鱼的市场价格与鱼池的产量均具有随机性,且互不影响,其具体情况如下表:
元,此鱼的市场价格与鱼池的产量均具有随机性,且互不影响,其具体情况如下表:
鱼池产量( ) ) |
 |
 |
鱼的市场价格(元/ ) ) |
 |
 |
|
| 概率 |
 |
 |
概率 |
 |
 |
(1)设 表示在这个鱼池养殖
表示在这个鱼池养殖 季这种鱼的利润,求
季这种鱼的利润,求 的分布列和期望;
的分布列和期望;
(2)若在这个鱼池中连续 季养殖这种鱼,求这
季养殖这种鱼,求这 季中至少有
季中至少有 季的利润不少于
季的利润不少于 元的概率.
元的概率.
某高校共有学生 人,其中男生
人,其中男生 人,女生
人,女生 人.为调查该校学生
人.为调查该校学生
每周平均体育运动时间的情况,采用分层抽样的方法,收集 位学生每周平均体育运动时间的样本数据(单位:小时).
位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这 个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:
个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为: ,
, ,
, ,
, ,
,
 .估计该校学生每周平均体育运动时间超过
.估计该校学生每周平均体育运动时间超过 小时的概率;
小时的概率;
(3)在样本数据中,有 位女生的每周平均体育运动时间超过
位女生的每周平均体育运动时间超过 小时,请完成每周平均体育运动时间与性别列联表,并判断是否有
小时,请完成每周平均体育运动时间与性别列联表,并判断是否有 %的把握认为“该校学生的每周平均体育运动时间与性别有关”.
%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
用 ,
, ,
,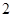 ,
, ,
,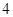 这五个数字组成无重复数字的自然数.
这五个数字组成无重复数字的自然数.
(1)在组成的三位数中,求所有偶数的个数;
(2)在组成的三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如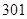 ,
, 等都是“凹数”,试求“凹数”的个数;
等都是“凹数”,试求“凹数”的个数;
(3)在组成的五位数中,求恰有一个偶数数字夹在两个奇数数字之间的自然数的个数.
已知 ,求:
,求:
(1) ;
;
(2) .
.
设函数 ,其中
,其中 为正实数.
为正实数.
(Ⅰ)若 是函数
是函数 的极值点,讨论函数
的极值点,讨论函数 的单调性;
的单调性;
(Ⅱ)若 在
在 上无最小值,且
上无最小值,且 在
在 上是单调增函数,求
上是单调增函数,求 的取值范围,并由此判断曲线
的取值范围,并由此判断曲线 与曲线
与曲线 在
在 交点个数.
交点个数.