一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有3、4、5、 ,甲、乙两人每次同时从袋中各随机摸出1个小球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复实验,实验数据如下表:
,甲、乙两人每次同时从袋中各随机摸出1个小球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复实验,实验数据如下表:
解答下列问题:如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近,估计出现“和为8”的概率是 。
如果摸出的这两
 个小球上数字之和为9的概率是
个小球上数字之和为9的概率是 ,那么
,那么 的值可以取7吗?请
的值可以取7吗?请 用列表法或画树状图说明理由;如果
用列表法或画树状图说明理由;如果 的值不可以取7,请写出一个符合要求的
的值不可以取7,请写出一个符合要求的 值。
值。
在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系(不要求证明);
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论.
如图,有两个 的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求:
的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求:
(1)线段的一个端点为梯形的顶点,另一个端点在梯形一边的格点上;
(2)将梯形分成两个图形,其中一个是轴对称图形;
(3)图1、图2中分成的轴对称图形不全等.
分解因式:(1) ;(2)
;(2) .
.
先化简,再求值: ,其中
,其中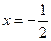
已知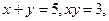 则
则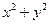 =""
=""