(本小题满分12分)已知点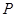 为
为 轴上的动点,点
轴上的动点,点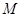 为
为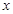 轴上的动点.点
轴上的动点.点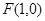 为定点,且满足
为定点,且满足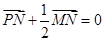 ,
,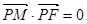
(Ⅰ)求动点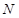 的轨迹
的轨迹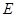 的方程.
的方程.
(Ⅱ)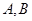 是
是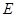 上的两个动点,
上的两个动点,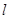 为
为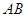 的中垂线,求当
的中垂线,求当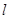 的斜率为2时,
的斜率为2时,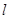 在
在 轴上的截距
轴上的截距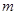 的范围.
的范围.
(本小题满分12分)为了分流地铁高峰的压力,市发改委通过听众会,决定实施低峰优惠票价制度.不超过 公里的地铁票价如下表:
公里的地铁票价如下表:
乘坐里程 (单位: (单位: ) ) |
 |
 |
 |
| 票价(单位:元) |
 |
 |
 |
现有甲、乙两位乘客,他们乘坐的里程都不超过 公里.已知甲、乙乘车不超过
公里.已知甲、乙乘车不超过 公里的概率分别为
公里的概率分别为 ,
, ,甲、乙乘车超过
,甲、乙乘车超过 公里且不超过
公里且不超过 公里的概率分别为
公里的概率分别为 ,
, .
.
(Ⅰ)求甲、乙两人所付乘车费用不相同的概率;
(Ⅱ)设甲、乙两人所付乘车费用之和为随机变量 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
(本小题满分12分)如图1,在矩形 中,
中,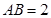 ,
, ,将
,将 沿矩形的对角线
沿矩形的对角线 翻折,得到如图2所示的几何体
翻折,得到如图2所示的几何体 ,使得
,使得 =
= .
.
(Ⅰ)求证: ;
;
(Ⅱ)若在 上存在点
上存在点 ,使得
,使得 ,求二面角
,求二面角 的余弦值.
的余弦值.
(本小题满分12分)数列 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,对于任意
项和,对于任意 ,总有
,总有 成等差数列.
成等差数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.
设集合 ,集合
,集合 ,
,
集合 中满足条件“
中满足条件“ ”的元素个数记为
”的元素个数记为 .
.
(1)求 和
和 的值;
的值;
(2)当 时,求证:
时,求证:
 .
.