已知函数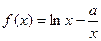 。
。
(Ⅰ)讨论函数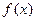 的单调区间;
的单调区间;
(Ⅱ)若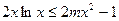 在
在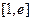 恒成立,求
恒成立,求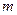 的取值范围。
的取值范围。
如图,已知平行六面体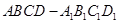 中,底面
中,底面 是边长为
是边长为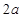 的菱形,侧棱
的菱形,侧棱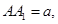 且
且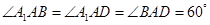 ;
;
(Ⅰ)求证: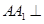 平面
平面 及直线
及直线 与平面
与平面 所成角;
所成角;
(Ⅱ)求侧面 与侧面
与侧面 所成的二面角的大小的余弦值
所成的二面角的大小的余弦值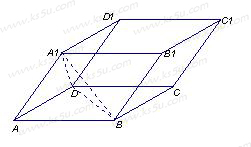
本题满分14分)设 ,圆
,圆 :
: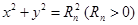 与
与 轴正半轴的交点为
轴正半轴的交点为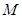 ,与曲线
,与曲线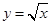 的交点为
的交点为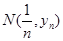 ,直线
,直线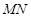 与
与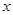 轴的交点为
轴的交点为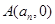 .
.
(Ⅰ)求证: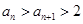 ;
;
(Ⅱ)设 ,
,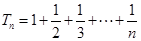 ,求证:
,求证: .
.
已知函数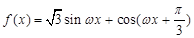

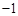
( ),且函数
),且函数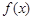 的最小正周期为
的最小正周期为 .
.
(Ⅰ)求函数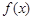 的解析式;
的解析式;
(Ⅱ)在△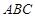 中,角
中,角 所对的边分别为
所对的边分别为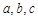 .若
.若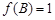 ,
,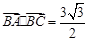 ,且
,且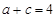 ,试求
,试求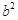 的值.
的值.
已知 ,直线l:
,直线l: ,椭圆C:
,椭圆C: ,
, ,
, 分别为椭圆C的左、右焦点。
分别为椭圆C的左、右焦点。
(Ⅰ)当直线l过右焦点 时,求直线l的方程;
时,求直线l的方程;
(Ⅱ)设直线l与椭圆C交于A,B两点。
(ⅰ)求线段AB长度的最大值;
(ⅱ) ,
, 的重心分别为G,H。若原点O在以线段GH为直径的圆内,求实数
的重心分别为G,H。若原点O在以线段GH为直径的圆内,求实数 的取值范围。
的取值范围。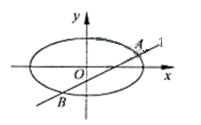
已知曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差是1。
(Ⅰ)求曲线C的方程;
(Ⅱ)过点K(-1,0)的直线l与C相交于A、B两点,点A关于x轴的对称点为D。证明:点F在直线BD上;