已知 ,直线l:
,直线l: ,椭圆C:
,椭圆C: ,
, ,
, 分别为椭圆C的左、右焦点。
分别为椭圆C的左、右焦点。
(Ⅰ)当直线l过右焦点 时,求直线l的方程;
时,求直线l的方程;
(Ⅱ)设直线l与椭圆C交于A,B两点。
(ⅰ)求线段AB长度的最大值;
(ⅱ) ,
, 的重心分别为G,H。若原点O在以线段GH为直径的圆内,求实数
的重心分别为G,H。若原点O在以线段GH为直径的圆内,求实数 的取值范围。
的取值范围。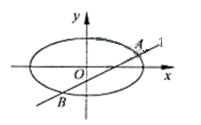
.设函数y=x3+ax2+bx+c的图象如图所示,且与y=0在原点相切,若函数的极小值为-4,(1)求a、b、c的值;(2)求函数的递减区间.
.(12分)设f(x)=x3+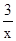 ,求函数f(x)的单调区间及其极值;
,求函数f(x)的单调区间及其极值;
(14分)已知中心在原点,顶点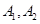 在
在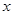 轴上,离心率为
轴上,离心率为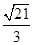 的双曲线经过点
的双曲线经过点 (I)求双曲线的方程(II)动直线
(I)求双曲线的方程(II)动直线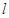 经过
经过 的重心
的重心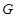 ,与双曲线交于不同的两点
,与双曲线交于不同的两点 ,问是否存在直线
,问是否存在直线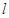 使
使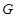 平分线段
平分线段 。试证明你的结论。
。试证明你的结论。
( 13分)某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为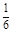 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。
(Ⅰ)求甲中奖且乙、丙都没有中奖的概率;
(Ⅱ)求中奖人数ξ的分布列及数学期望Eξ.
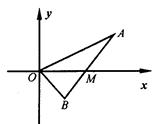
如图,线段AB过x轴正半轴上一定点M(m,0),端点A、B到x轴的距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线,求该抛物线的方程。