.(12分)设f(x)=x3+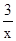 ,求函数f(x)的单调区间及其极值;
,求函数f(x)的单调区间及其极值;
已知数列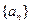 满足
满足 ,且
,且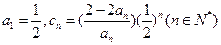 .
.
(Ⅰ)求证:数列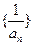 是等差数列,并求通项
是等差数列,并求通项 ;
;
(Ⅱ)求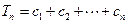 的值;
的值;
已知等差数列 的首项
的首项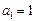 ,公差
,公差 .且
.且 分别是等比数列
分别是等比数列 的
的
 .
.
(1)求数列 与
与 的通项公式;
的通项公式;
(2)设数列 对任意自然数
对任意自然数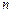 均有:
均有: 成立.求
成立.求 的值。
的值。
已知 的三内角A,B,C所对三边分别为a,b,c,且
的三内角A,B,C所对三边分别为a,b,c,且
(I)求 的值。
的值。
(II)若 的面积
的面积 求a的值。
求a的值。
假设国家收购某种农产品的价格是1.2元/kg,其中征税标准为每100元征8元(即税率为8个百分点,8%),计划可收购 kg.为了减轻农民负担,决定税率降低
kg.为了减轻农民负担,决定税率降低 个百分点,预计收购可增加
个百分点,预计收购可增加 个百分点.
个百分点.
(1)写出税收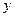 (元)与
(元)与 的函数关系;
的函数关系;
(2)要使此项税收在税率调节后不低于原计划的78%,确定 的取值范围.
的取值范围.
在 中,已知
中,已知 ,
, .
. (Ⅰ)求
(Ⅰ)求 的值;
的值;
(Ⅱ)若 为
为 的中点,求
的中点,求 的长.
的长.