( 13分)某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为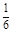 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。
(Ⅰ)求甲中奖且乙、丙都没有中奖的概率;
(Ⅱ)求中奖人数ξ的分布列及数学期望Eξ.
已知圆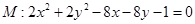 ,直线
,直线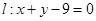 ,过
,过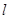 上一点A作
上一点A作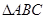 ,使得
,使得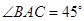 ,边AB过圆心M,且B,C在圆M上,求点A纵坐标的取值范围。
,边AB过圆心M,且B,C在圆M上,求点A纵坐标的取值范围。
某跨国饮料公司对全世界所有人均GDP(即人均纯收入)在0.5—8千美元的地区销售,该公司M饮料的销售情况的调查中发现:人均GDP处在中等的地区对该饮料的销售量最多,然后向两边递减.
(1)下列几个模拟函数中(x表示人均GDP,单位:千美元;y表示年人均M饮料的销量,单位:升),用哪个来描述人均,饮料销量与地区的人均GDP的关系更合适?说明理由.
A.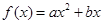 |
B.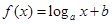 |
C.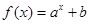 |
D.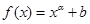 |
(2)若人均GDP为1千美元时,年人均M饮料的销量为2升;人均GDP为4千美元时,年人均M饮料的销量为5升;把你所选的模拟函数求出来.;
(3)因为M饮料在N国被检测出杀虫剂的含量超标,受此事件影响,M饮料在人均GDP不高于3千美元的地区销量下降5%,不低于6千美元的地区销量下降5%,其他地区的销量下降10%,根据(2)所求出的模拟函数,求在各个地区中,年人均M饮料的销量最多为多少?
如图C,D是以AB为直径的圆上的两点,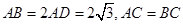 ,F是AB上的一点,且
,F是AB上的一点,且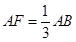 ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知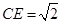

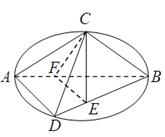
(1)求证:AD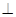 平面BCE
平面BCE
(2)求证:AD//平面CEF;
(3)求三棱锥A-CFD的体积.
已知 的顶点
的顶点 ,过点
,过点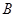 的内角平分线所在直线方程是
的内角平分线所在直线方程是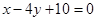 ,过点C的中线所在直线的方程是
,过点C的中线所在直线的方程是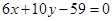
(1)求顶点B的坐标;(2)求直线BC的方程;
已知函数
(1)若 ,求
,求 的值;
的值;
(2)求 的值.
的值.