(本小题满分14分)设二次函数 满足下列条件:
满足下列条件:
①当 ∈R时,
∈R时, 的最小值为0,且f (
的最小值为0,且f ( -1)=f(-
-1)=f(- -1)成立;
-1)成立;
②当 ∈(0,5)时,
∈(0,5)时, ≤
≤ ≤2
≤2 +1恒成立。
+1恒成立。
(1)求 的值;
的值;
(2)求 的解析式;
的解析式;
(3)求最大的实数m(m>1),使得存在实数t,只要当 ∈
∈ 时,就有
时,就有 成立。
成立。
已知函数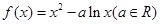
(1)若 ,求函数
,求函数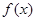 的极值;
的极值;
(2)已知函数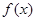 在点
在点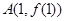 处的切线为
处的切线为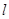 ,若此切线在点A处穿过
,若此切线在点A处穿过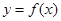 的图像(即函数
的图像(即函数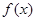 上的动点P在点A附近沿曲线
上的动点P在点A附近沿曲线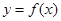 运动,经过点A时从
运动,经过点A时从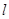 的一侧进入另一侧),求函数
的一侧进入另一侧),求函数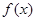 的表达式;
的表达式;
(3)若 ,函数
,函数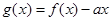 有且仅有一个零点,求实数
有且仅有一个零点,求实数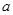 的值.
的值.
已知椭圆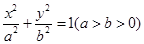 ,F为椭圆的右焦点,点A,B分别为椭圆的上下顶点,过点B作AF的垂线,垂足为M.
,F为椭圆的右焦点,点A,B分别为椭圆的上下顶点,过点B作AF的垂线,垂足为M.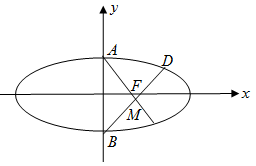
(1)若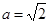 ,
,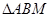 的面积为1,求椭圆方程;
的面积为1,求椭圆方程;
(2)是否存在椭圆,使得点B关于直线AF对称的点D仍在椭圆上,若存在,求椭圆的离心率的值;若不存在,说明理由.
如图,地图上有一竖直放置的圆形标志物,圆心为C,与地面的接触点为G.与圆形标志物在同一平面内的地面上点P处有一个观测点,且PG=50m.在观测点正前方10m处(即PD=10m)有一个高位10m(即ED=10m)的广告牌遮住了视线,因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧.
(1)若圆形标志物半径为25m,以PG所在直线为X轴,G为坐标原点,建立直角坐标系,求圆C和直线PF的方程;
(2)若在点P处观测该圆形标志的最大视角(即 )的正切值为
)的正切值为 ,求该圆形标志物的半径.
,求该圆形标志物的半径.
已知直线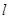 与圆
与圆 相交于A,B两点,弦AB的中点为
相交于A,B两点,弦AB的中点为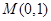
(1)求实数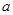 的取值范围以及直线
的取值范围以及直线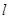 的方程;
的方程;
(2)若以AB为直径的圆过原点O,求圆C的方程.
在 中,
中, ,D是边BC上一点,
,D是边BC上一点,
(1)求 的值;
的值;
(2)求 的值
的值