温州市有一种可食用的野生菌，上市时，外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中，据预测，该野生菌的市场价格将以每天每千克上涨1元；但冷冻存放这批野生菌时每天需要支出各种费用合计310元，而且这类野生菌在冷库中最多保存160天，同时，平均每天有3千克的野生菌损坏不能出售。设
天后每千克该野生菌的市场价格为
元，试写出与之间的函数关系式；若存放
天后，将这批野生菌一次性出售，设这批野生菌的销售总额为
元，试写出与之间的函数关系式；李经理将这批野生菌存放多少天后出售可获得最大利润
元？
（利润＝销售总额－收购成本－各种费用）
计算：
．
计算: （-1)2015+sin300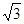+(2-
）(2+）．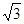
计算：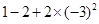
．
如图，在▱ABCD中，对角线AC、BD相交于点O，点E、F是AD上的点，且AE=EF=FD．连接BE、BF，使它们分别与AO相交于点G、H．
（1）求EG：BG的值；
（2）求证：AG=OG；
（3）设AG=a，GH=b，HO=c，求a：b：c的值．
如图，折叠矩形OABC的一边BC，使点C落在OA边的点D处，已知折痕BE=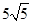
，且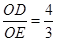
，以O为原点，OA所在的直线为x轴建立如图所示的平面直角坐标系，抛物线l：
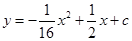经过点E，且与AB边相交于点F．
（1）求证：△ABD∽△ODE；
（2）若M是BE的中点，连接MF，求证：MF⊥BD；
（3）P是线段BC上一点，点Q在抛物线l上，且始终满足PD⊥DQ，在点P运动过程中，能否使得PD=DQ？若能，求出所有符合条件的Q点坐标；若不能，请说明理由．