已知数列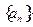 的前
的前 项和为
项和为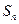 ,且
,且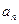 是
是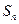 与2的等差中项 ;数列
与2的等差中项 ;数列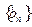 中,
中,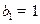 ,点
,点 在直线
在直线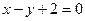 上。
上。
(Ⅰ) 求数列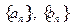 的通项公式
的通项公式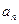 和
和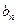 ;
;
(Ⅱ)设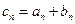 ,求数列
,求数列 的前n项和
的前n项和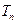
用反证法证明:如果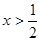 ,那么
,那么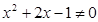 .
.
已知函数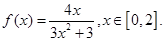
(Ⅰ)求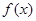 的值域;
的值域;
(Ⅱ)设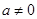 ,函数
,函数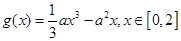 .若对任意
.若对任意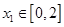 ,总存在
,总存在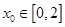 ,使
,使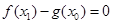 ,求实数
,求实数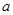 的取值范围.
的取值范围.
某种项目的射击比赛,开始时在距目标100m处射击,如果命中记3分,且停止射击;若第一次射击未命中,可以进行第二次射击,但目标已在150m处,这时命中记2分,且停止射击;若第二次仍未命中,还可以进行第三次射击,此时目标已在200m处,若第三次命中则记1分,并停止射击;若三次都未命中,则记0分,且比赛结束.已知射手甲在100m处击中目标的概率为 ,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
(1)求射手甲在这次射击比赛中命中目标的概率;
(2)求射手甲在这次射击比赛中得分的数学期望.
如图,在长方体 中,
中, 分别是
分别是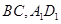 的中点,
的中点, 分
分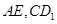 的中点,
的中点,

(Ⅰ)求证: 面
面 ;
;
(Ⅱ)求二面角 的大小。
的大小。
(Ⅲ)求三棱锥 的体积。
的体积。
已知定义在R上的函数f(x)=x2(ax-3),其中a为常数.
(Ⅰ)若x=1是函数f(x)的一个极值点,求a的值;
(Ⅱ)若函数f(x)在区间(-1,0)上是增数,求a的取值范围.