(本小题满分10分)选修4-5:不等式选讲
设函数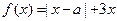 ,其中
,其中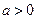 ,
,
(1)当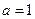 时,求不等式
时,求不等式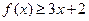 的解集
的解集
(2)若不等式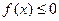 的解集为
的解集为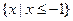 ,求
,求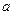 的值.
的值.
设有关于 的一元二次方程
的一元二次方程 .
.
(1)若 是从集合
是从集合 中任取一个元素,
中任取一个元素, 是从集合
是从集合 中任取一个元素,求方程
中任取一个元素,求方程 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;
(2)若 是从集合
是从集合 中任取一个元素,
中任取一个元素, 是从集合
是从集合 中任取一个元素,求上述方程有实根的概率.
中任取一个元素,求上述方程有实根的概率.
命题 :关于
:关于 的不等式
的不等式 的解集为
的解集为 ;,命题
;,命题 :函数
:函数 为增函数.如果命题“
为增函数.如果命题“ ”为真命题,“
”为真命题,“ ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
如图,椭圆 的一个焦点是
的一个焦点是 ,
, 为坐标原点.
为坐标原点.
(1)已知椭圆短轴的两个三等分点 与一个焦点构成正三角形,求椭圆的方程;
与一个焦点构成正三角形,求椭圆的方程;
(2)设过点 的直线
的直线 交椭圆于
交椭圆于 两点.若直线
两点.若直线 绕点
绕点 任意转动,则有
任意转动,则有 ,求
,求 的取值范围.
的取值范围.
已知椭圆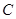 :
: 的右焦点
的右焦点 ,过
,过 的直线交椭圆
的直线交椭圆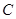 于
于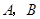 两点,且
两点,且 是线段
是线段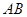 的中点.
的中点.
(1)求椭圆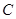 的方程;
的方程;
(2)已知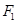 是椭圆的左焦点,求
是椭圆的左焦点,求 的面积.
的面积.
学校从参加高二年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及各组频数如下:
[40,50),2;[50,60),3;[60,70),14;[70,80),15;[80,90),12;[90,100],4.
| 分组 |
频数 |
频率 |
| [40,50) |
2 |
0.04 |
| [50,60) |
3 |
0.06 |
| [60,70) |
14 |
0.28 |
| [70,80) |
15 |
0.30 |
| [80,90) |
A |
B |
| [90,100] |
4 |
0.08 |
| 合计 |
C |
D |
(1)在给出的样本频率分布表中,求 的值;
的值;
(2)估计成绩在80分以上(含80分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在[90,100]的学生中选两位同学,共同帮助成绩在[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.
样本频率分布表如下: