椭圆 经过点
经过点 ,对称轴为坐标轴,焦点
,对称轴为坐标轴,焦点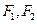 在
在 轴上,离心率
轴上,离心率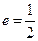 ,
,
求椭圆 的方程。
的方程。
(本小题共14分)
已知 ,动点
,动点 到定点
到定点
 的距离比
的距离比 到定直线
到定直线 的距离小
的距离小 .
.
(I)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设 是轨迹
是轨迹 上异于原点
上异于原点 的两个不同点,
的两个不同点, ,求
,求 面积的最小值;
面积的最小值;
(Ⅲ)在轨迹 上是否存在两点
上是否存在两点 关于直线
关于直线 对称?若存在,求出直线
对称?若存在,求出直线 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
(本小题共14分)
已知函数 .
.
(I)判断函数 的单调性;
的单调性;
(Ⅱ)若
 +
+ 的图像总在直线
的图像总在直线 的上方,求实数
的上方,求实数 的取值范围;
的取值范围;
(Ⅲ)若函数 与
与 的图像有公共点,且在公共点处的切线相同,求实数
的图像有公共点,且在公共点处的切线相同,求实数 的值.
的值.
(本小题共13分)
设 是正数组成的数列,其前
是正数组成的数列,其前 项和为
项和为 ,且对于所有的正整数
,且对于所有的正整数 ,有
,有 .
.
(I) 求 ,
, 的值;
的值;
(II) 求数列 的通项公式;
的通项公式;
(III)令 ,
, ,
, (
( ),求数列
),求数列 的前
的前 项和
项和 .
.
(本小题共13分)
在一次考试中共有8道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的.某考生有4道题已选对正确答案,其余题中有两道只能 分别判断2个选项是错误的,还有两道题因不理解题意只好乱猜.
分别判断2个选项是错误的,还有两道题因不理解题意只好乱猜.
(Ⅰ) 求该考生8道题全答对的概率;
(Ⅱ)
若评分标准规定:“每题只选一个选项,选对得5分,不选或选错得0分”,求该考生所得分数的分布列.
(本小题共13分)
已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中标出的数据,
(Ⅰ)求这个组合体的表面积;
(Ⅱ)若组合体的底部几何体记为 ,其中
,其中 为正方形.
为正方形.
(i)求证: ;
;
(ii)设点 为棱
为棱 上
上 一点,求直线
一点,求直线 与平面
与平面 所成角的正弦值的取值范围.
所成角的正弦值的取值范围.
