抛物线 的焦点为F,点A、B在抛物线上(A点在第一象限,B点在第四象限),且|FA|=2,|FB|=5,
的焦点为F,点A、B在抛物线上(A点在第一象限,B点在第四象限),且|FA|=2,|FB|=5,
求:(1)点A、B的坐标
(2)线段AB的长度和直线AB的方程;
设 是以
是以 为焦点的抛物线
为焦点的抛物线 ,
, 是以直线
是以直线 与
与 为渐近线,以
为渐近线,以 为一个焦点的双曲线.
为一个焦点的双曲线.
(1)求双曲线 的标准方程;
的标准方程;
(2)若 与
与 在第一象限内有两个公共点
在第一象限内有两个公共点 和
和 ,求
,求 的取值范围,并求
的取值范围,并求 的最大值;
的最大值;
(3)若 的面积
的面积 满足
满足 ,求
,求 的值.
的值.
如图,在三棱锥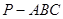 中,
中,
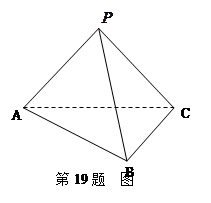
(1)求证:平面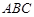 ⊥平面
⊥平面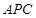
(2)求直线PA与平面PBC所成角的正弦值;
(3)若动点M在底面三角形ABC上,二面角M-PA-C的余弦值为 ,求BM的最小值.
,求BM的最小值.
如图所示,质点P在正方形ABCD的四个顶点上按逆时针方向前进.现在投掷一个质地均匀、每个面上标有一个数字的正方体玩具,它的六个面上分别写有两个1、两个2、两个3一共六个数字.质点P从A点出发,规则如下:当正方体上底面出现的数字是1,质点P前进一步(如由A到B);当正方体上底面出现的数字是2,质点P前进两步(如由A到C),当正方体上底面出现的数字是3,质点P前进三步(如由A到D).在质点P转一圈之前连续投掷,若超过一圈,则投掷终止.
(1)求质点P恰好返回到A点的概率;
(2)在质点P转一圈恰能返回到A点的所有结果中,用随机变量ξ表示点P恰能返回到A点的投掷次数,求ξ的数学期望.
阅读下面材料:
根据两角和与差的正弦公式,有 ------①
------①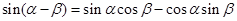 ------②
------②
由①+② 得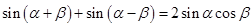 ------③
------③
令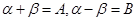 有
有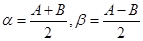
代入③得 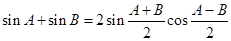 .
.
(Ⅰ) 类比上述推理方法,根据两角和与差的余弦公式,证明: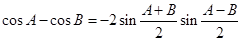 ;
;
(Ⅱ)若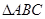 的三个内角
的三个内角 满足
满足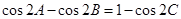 ,试判断
,试判断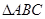 的形状.
的形状.
(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
已知函数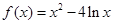 ,
, ;
;
(1)求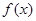 在
在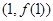 处的切线方程;
处的切线方程;
(2)若 有唯一解,求
有唯一解,求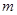 的取值范围;
的取值范围;
(3)是否存在实数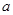 ,使得
,使得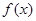 与
与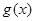 在
在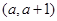 上均为增函数,若存在求出
上均为增函数,若存在求出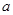 的范围,若不存在请说明理由
的范围,若不存在请说明理由