阅读下面材料:
根据两角和与差的正弦公式,有 ------①
------①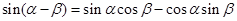 ------②
------②
由①+② 得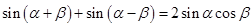 ------③
------③
令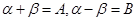 有
有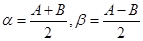
代入③得 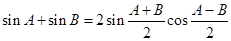 .
.
(Ⅰ) 类比上述推理方法,根据两角和与差的余弦公式,证明: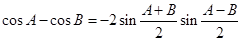 ;
;
(Ⅱ)若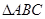 的三个内角
的三个内角 满足
满足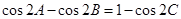 ,试判断
,试判断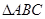 的形状.
的形状.
(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
已知函数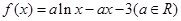 .
.
(1)当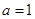 时,求函数
时,求函数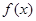 的单调区间;
的单调区间;
(2)若函数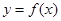 的图象在点
的图象在点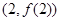 处的切线的倾斜角为
处的切线的倾斜角为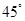 ,问:实数
,问:实数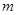 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的 ,函数
,函数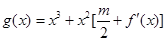 在区间
在区间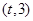 上总存在极值?
上总存在极值?
在 中,三个内角
中,三个内角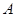 、
、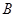 、
、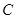 对应的边分别为
对应的边分别为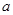 、
、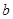 、
、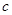 ,
,
(1)若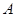 、
、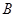 、
、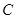 成等差数列,且
成等差数列,且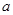 、
、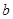 、
、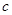 成等比数列,求证:
成等比数列,求证: 为等边三角形
为等边三角形
(2)若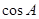 、
、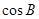 、
、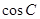 成等比数列,
成等比数列,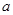 、
、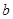 、
、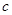 成等比数列,求证:
成等比数列,求证: 为等边三角形
为等边三角形
在极坐标系中,已知某曲线C的极坐标方程为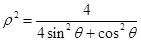 ,直线
,直线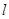 的极坐标方程为
的极坐标方程为
(1)求该曲线C的直角坐标系方程及离心率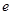
(2)已知点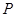 为曲线C上的动点,求点
为曲线C上的动点,求点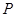 到直线
到直线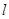 的距离的最大值。
的距离的最大值。
中山纪念中学高二A、B两个班参加了2012年的“广州一模数学考试”,按照成绩大于等于125分为“优秀”,成绩小于125分为“非优秀”, 根据调查这两个班的数学成绩得到的数据,所绘制的二维条形图如图.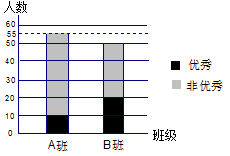
(1)根据图中数据,制作2×2列联表;
(2)计算随机变量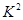 的值(精确到0.001)
的值(精确到0.001)
(3)判断在多大程度上可以认为“成绩与班级有关系”? (温馨提示:答题前请仔细阅读卷首所给的计算公式及其参考值)
在复平面内,复数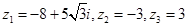 所对应的点为
所对应的点为 、
、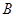 、
、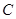 ,以
,以 、
、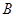 、
、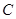 为顶点的三角形为
为顶点的三角形为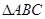
(1)求 ;
;
(2)求以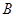 、
、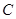 为焦点且过点
为焦点且过点 的双曲线的方程.
的双曲线的方程.