有一个数学活动,其具体操作过程是:
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开
(如图1);
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图2).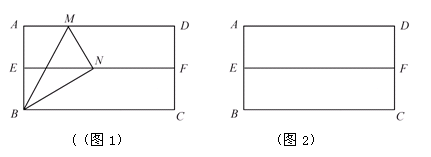
请解答以下问题:如图2,若延长MN交线段BC于P,△BMP是什么三角形?请证明你的结论.
在图2中,若AB=a,BC=b,a、b满足什么关系,才能在矩形纸片ABCD上剪出符合(1)中结论的三角形纸片BMP
若m满足式子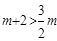 ,试判断关于x的一元二次方程
,试判断关于x的一元二次方程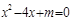 的根的情况
的根的情况
一天晚上,小明帮助姐姐清洗两套只有颜色不同的有盖茶杯,此时突然停电了,小明只好把杯盖和茶杯随机地搭配在一起,请用列表法或树形图法求出颜色搭配正确的概率
如图,抛物线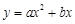 (a
(a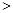 0)与双曲线
0)与双曲线 相交于点A,B. 已知点A的坐标为
相交于点A,B. 已知点A的坐标为
(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).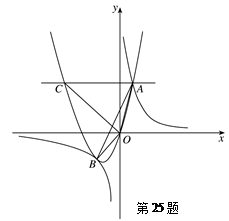
求实数a,b,k的值;
过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,求所有满足△EOC∽△AOB的点E的坐标.(其中点E和点A,点C和点B分别是对应点)
在边长为10的正方形ABCD中,以AB为直径作半圆O,如图①,E是半圆上一动点,过点E作EF⊥AB,垂足为F,连结DE.
当DE=10时,求证:DE与圆O相切;
求DE的最长距离和最短距离;
如图②,建立平面直角坐标系,当DE =10时,试求直线DE的解析式.
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°,C岛在B岛的北偏西40°,A、B两岛相距100km.
求从C岛看A、B两岛的视角∠ACB的度数;
已知海洋保护区的范围设在以C点为圆心,40km
为半径的圆形区域内.如果一艘轮船从A岛直线航
行到B岛,那么它会不会穿越保护区.为什么?