如图,在平面直角坐标系中,四边形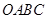 为矩形,
为矩形,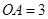 ,
,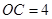 ,
,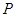 为直线
为直线 上一动点,将直线
上一动点,将直线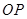 绕点
绕点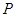 逆时针方向旋转
逆时针方向旋转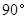 交直线
交直线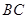 于点
于点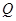 ;
;
当点
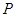 在线段
在线段 上运动(不与
上运动(不与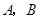 重合)时,
重合)时,
求证:OA·BQ=AP·BP;在(1)成立的条件下,设点
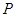 的横坐标为
的横坐标为 ,
,
线段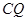 的长度为
的长度为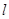 ,求出
,求出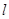 关于
关于 的函数解析式,
的函数解析式,
并判断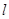 是否存在最小值,若存在,请求出最小值;
是否存在最小值,若存在,请求出最小值;
若不存在,请说明理由。直线
 上是否存在点
上是否存在点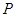 ,使
,使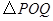 为等腰三角形,若存在,
为等腰三角形,若存在,
请求出点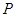 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
(绵阳)如图,在边长为2的正方形ABCD中,G是AD延长线时的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长AG于N.
(1)是否存在点M,使△ABM为等腰三角形?若存在,分析点M的位置;若不存在,请说明理由;
(2)当点N在AD边上时,若BN⊥HN,NH交∠CDG的平分线于H,求证:BN=HN;
(3)过点M分别作AB,AD的垂线,垂足分别为E,F,矩形AEMF与△ACG重叠部分的面积为S,求S的最大值.
(眉山)(本小题满分11分)如图,已知抛物线 的顶点D的坐标为(1,
的顶点D的坐标为(1, ),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
(l)求抛物线所对应的二次函数的表达式;
(2)若动点P满足∠PAO不大于45°,求P点的横坐标m的取值范围;
(3)当P点的横坐标 时,过p点作y轴的垂线PQ,垂足为Q.问:是否存在P点,使∠QPO=∠BCO?若存在,请求出P点的坐标;若不存在,请说明理由.
时,过p点作y轴的垂线PQ,垂足为Q.问:是否存在P点,使∠QPO=∠BCO?若存在,请求出P点的坐标;若不存在,请说明理由.
(泸州)如图,已知二次函数的图象M经过A(﹣1,0),B(4,0),C(2,﹣6)三点.
(1)求该二次函数的解析式;
(2)点G是线段AC上的动点(点G与线段AC的端点不重合),若△ABG与△ABC相似,求点G的坐标;
(3)设图象M的对称轴为l,点D(m,n)( )是图象M上一动点,当△ACD的面积为
)是图象M上一动点,当△ACD的面积为 时,点D关于l的对称点为E,能否在图象M和l上分别找到点P、Q,使得以点D、E、P、Q为顶点的四边形为平行四边形?若能,求出点P的坐标;若不能,请说明理由.
时,点D关于l的对称点为E,能否在图象M和l上分别找到点P、Q,使得以点D、E、P、Q为顶点的四边形为平行四边形?若能,求出点P的坐标;若不能,请说明理由.
(宜宾)如图,抛物线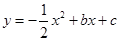 与x轴分别相交于点A(﹣2,0),B(4,0),与y轴交于点C,顶点为点P.
与x轴分别相交于点A(﹣2,0),B(4,0),与y轴交于点C,顶点为点P.
(1)求抛物线的解析式;
(2)动点M、N从点O同时出发,都以每秒1个单位长度的速度分别在线段OB、OC上向点B、C方向运动,过点M作x轴的垂线交BC于点F,交抛物线于点H.
①当四边形OMHN为矩形时,求点H的坐标;
②是否存在这样的点F,使△PFB为直角三角形?若存在,求出点F的坐标;若不存在,请说明理由.
(遂宁)如图,一次函数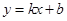 与反比例函数
与反比例函数 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.