(绵阳)如图,在边长为2的正方形ABCD中,G是AD延长线时的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长AG于N.
(1)是否存在点M,使△ABM为等腰三角形?若存在,分析点M的位置;若不存在,请说明理由;
(2)当点N在AD边上时,若BN⊥HN,NH交∠CDG的平分线于H,求证:BN=HN;
(3)过点M分别作AB,AD的垂线,垂足分别为E,F,矩形AEMF与△ACG重叠部分的面积为S,求S的最大值.
(1)解方程:3x2-27=0
(2)已知22x+1+4x=48,求x的值.
(本题14分)已知抛物线
(1)填空:抛物线的顶点坐标是( ,),对称轴是 ;
(2)已知y轴上一点A(0,-2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;
(3)在(2)的条件下,点M在直线AP上.在平面内是否存在点 N,使以点O、点A、点M、点N为顶点的四边形为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由.
(本题12分) 某水果批发商场经销一种水果,如果每千克盈利10元,每天可售出400千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)当每千克涨价为多少元时,每天的盈利最多?最多是多少?
(2)若商场只要求保证每天的盈利为4420元,同时又可使顾客得到实惠,每千克应涨价为多少元?
(本题10分)如图,在⊙O中,弧AB=60°,AB=6,
(1)求圆的半径;
(2)求弧AB的长;
(3)求阴影部分的面积.
(本题10分)二次函数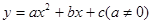 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题:
(1)写出方程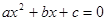 的两个根;
的两个根;
(2)当x为何值时,y>0;y<0?
(3)写出y随x的增大而减小的自变量x的取值范围.