如图,椭圆C: 焦点在
焦点在 轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C:分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线
轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C:分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线 上一点P.
上一点P.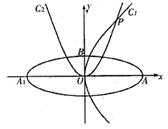
⑴求椭圆C及抛物线C1、C2的方程;
⑵若动直线 与直线OP垂直,且与椭圆C交于不同两点M、N,已知点Q(
与直线OP垂直,且与椭圆C交于不同两点M、N,已知点Q(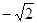 ,0),求
,0),求 的最小值.
的最小值.
设数列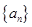 为等差数列,且
为等差数列,且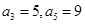 ;数列
;数列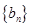 的前n项和为
的前n项和为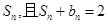 .
.
(1)求数列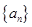 ,
,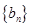 的通项公式;
的通项公式;
(2)若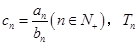 为数学
为数学 的前n项和,求
的前n项和,求 .
.
如图,在四棱锥中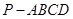 中,底面
中,底面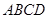 为菱形,
为菱形,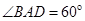 ,
,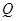 为
为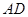 的中点.
的中点.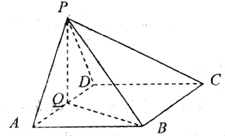
(1)若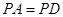 ,求证:平面
,求证:平面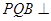 平面
平面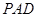 ;
;
(2)若平面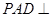 平面
平面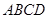 ,且
,且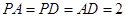 ,点
,点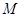 在线段
在线段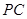 上,且
上,且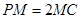 ,求三棱锥
,求三棱锥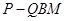 的体积.
的体积.
为了对某课题进行研究,用分层抽样方法从三所高校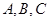 的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
| 高校 |
相关人数 |
抽取人数 |
| A |
18 |
x |
| B |
36 |
2 |
| C |
54 |
y |
(1)求 、
、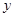 ;
;
(2)若从高校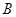 、
、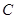 抽取的人中选2人作专题发言,求这2人都来自高校
抽取的人中选2人作专题发言,求这2人都来自高校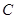 的概率.
的概率.
已知向量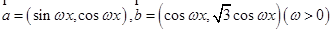 ,函数
,函数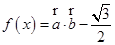 的最小正周期为
的最小正周期为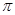 .
.
(1)求函数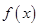 的单调增区间;
的单调增区间;
(2)如果△ABC的三边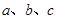 所对的角分别为
所对的角分别为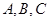 ,且满足
,且满足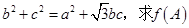 的值.
的值.
已知函数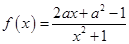 ,其中
,其中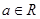 .
.
(1)当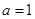 时,求曲线
时,求曲线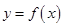 在原点处的切线方程;
在原点处的切线方程;
(2)求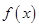 的单调区间;
的单调区间;
(3)若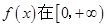 上存在最大值和最小值,求
上存在最大值和最小值,求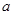 的取值范围.
的取值范围.