已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 的最大值及取得最大值的自变量
的最大值及取得最大值的自变量 的集合;
的集合;
(3)如何由函数 的图像通过适当的变换得到函数
的图像通过适当的变换得到函数 的图像,写出变换过程.
的图像,写出变换过程.
如图,△ABC中,AB=AC,AD是中线,P为AD上一点,CF∥AB,BP延长线交AC、CF于E、F,求证:PB2=PE·PF.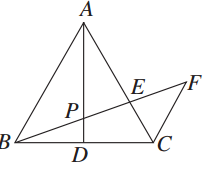
某企业为加大对新产品的推销力度,决定从今年起每年投入100万元进行广告宣传,以增加新产品的销售收入.已知今年的销售收入为250万元,经市场调查,预测第n年与第n-1年销售收入an与an-1(单位:万元)满足关系式:an=an-1+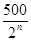 -100.
-100.
(1)设今年为第1年,求第n年的销售收入an;
(2)依上述预测,该企业前几年的销售收入总和Sn最大.
已知数列{an}中,a1=2,an-an-1-2n=0(n≥2,n∈N*).
(1)写出a2,a3的值(只写结果),并求出数列{an}的通项公式;
(2)设bn=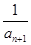 +
+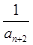 +
+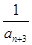 +…+
+…+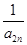 ,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+
,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+ >bn恒成立,求实数t的取值范围.
>bn恒成立,求实数t的取值范围.
已知数列{an}的前n项和为Sn,a1=2.当n≥2时,Sn-1+1,an,Sn+1成等差数列.
(1)求证:{Sn+1}是等比数列;
(2)求数列{nan}的前n项和Tn.
已知各项均不相等的等差数列{an}的前n项和为Sn,若S3=15,且a3+1为a1+1和a7+1的等比中项.
(1)求数列{an}的通项公式与前n项和Sn;
(2)设Tn为数列{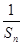 }的前n项和,问是否存在常数m,使Tn=m[
}的前n项和,问是否存在常数m,使Tn=m[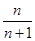 +
+ ],若存在,求m的值;若不存在,说明理由.
],若存在,求m的值;若不存在,说明理由.