为发展“低碳经济”，某单位进行技术革新, 让可再生资源重新利用. 从今年1月1日开始,该单位每月再生资源处理量y（吨）与月份x之间成如下一次函数关系：
| 月份x |
1 |
2 |
| 再生资源处理量y（吨） |
40 |
50 |
月处理成本z（元）与每月再生资源处理量y（吨）之间的函数关系可近似地表示为：
z =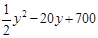
,每处理一吨再生资源得到的新产品的售价定为100元.该单位哪个月获得利润最大？最大是多少？
随着人们环保意识的增加，该单位需求的可再生资源数量受限。今年三、四月份的再生资源处理量都比二月份减少了m% ,该新产品的产量也随之减少，其售价都比二月份的售价增加了0.6m%.五月份，该单位得到国家科委的技术支持，使月处理成本比二月份的降低了20% .如果该单位在保持三月份的再生资源处理量和新产品售价的基础上，其利润是二月份的利润的一样,求m ．( m保留整数) （
如图，点O为矩形ABCD的对称中心，AB＝10cm，BC＝12cm．点E，F，G分别从A，B，C三点同时出发，沿矩形的边按逆时针方向匀速运动，点E的运动速度为1cm/s，点F的运动速度为3cm／s，点G的运动速度为1.5cm／s．当点F到达点C（即点F与点C重合）时，三个点随之停止运动．在运动过程中，△EBF关于直线EF的对称图形是△EB'F，设点E，F，G运动的时间为t（单位：s）．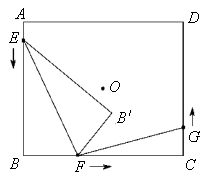
（1）当t＝ s时，四边形EBFB'为正方形；
（2）若以点E，B，F为顶点的三角形与以点F，C，G为顶点的三角形相似，求t的值；
（3）是否存在实数t，使得点B'与点O重合？若存在，求出t的值；若不存在，请说明理由．
如图，在Rt△ABC中，∠ACB＝900，点D是边AB上一点，以BD为直径的⊙O与边AC相切于点E，连接DE并延长DE交BC的延长线于点F．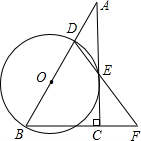
（1）求证：BD＝BF；
（2）若CF＝1，cosB＝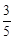
，求⊙O的半径．
如图，∴P是菱形ABCD对角线AC上的一点，连接DP并延长DP交边AB于点E，连接BP并延长BP交边AD于点F，交CD的延长线于点G．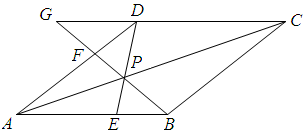
（1）求证：△APB≌△APD；
（2）已知DF：FA＝1：2，设线段DP的长为x，线段PF的长为y．
①求y与x的函数关系式；
②当x＝6时，求线段FG的长．
如图，在一笔直的海岸线l上有A，B两个观测站，A在B的正东方向，AB＝2（单位：km）．有一艘小船在点P处，从A测得小船在北偏西600的方向，从B测得小船在北偏东450的方向．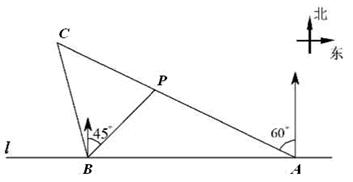
（1）求点P到海岸线l的距离；
（2）小船从点P处沿射线AP的方向航行一段时间后，到达点C处．此时，从B测得小船在北偏西150的方向．求点C与点B之间的距离．
（上述2小题的结果都保留根号）
如图，在方格纸中，△ABC的三个顶点及D，E，F，G，H五个点分别位于小正方形的顶点上．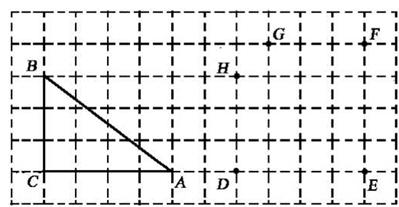
（1）现以D，E，F，G，H中的三个点为顶点画三角形，在所画的三角形中与△ABC不全等但面积相等的三角形是 （只需要填一个三角形）；
（2）先从D，E两个点中任意取一个点，再从F，G，H三个点中任意取两个不同的点，以所取的这三个点为顶点画三角形，求所画三角形与△ABC面积相等的概率（用画树状图或列表格求解）．