如图，一次函数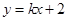
的图象与反比例函数
的
图象交于点P，点P在第一象限．PA⊥x轴于点A，PB⊥y
轴于点B．一次函数的图象分别交
轴、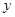
轴于点C、D，
且S△PBD=4，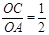
．求点D的坐标；
求一次函数与反比例函数的解析式；
根据图象写出在第一象限内一次函数的值小于反比例函数的值的
的取值范围.
已知m是方程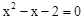
的一个实数根，求代数式
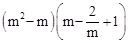的值．
为了提高产品的附加值，某公司计划将研发生产的1200件新产品进行精加工后再投放市场．现有甲、乙两个工厂都具备加工能力，公司派出相关人员分别到这两个工厂了解情况，获得如下信息：
信息一：甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天；
信息二：乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍．
根据以上信息，求甲、乙两个工厂每天分别能加工多少件新产品．
如图，在△ABC中，AB=CB，∠ABC=900，D为AB延长线上一点，点E在BC边上，且BE=BD，连结AE、DE、DC．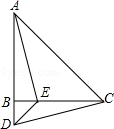
①求证：△ABE≌△CBD；
②若∠CAE=300，求∠BDC的度数．
解不等式组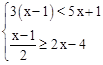
，并指出它的所有非负整数解．
如图1所示，已知直线
与x轴、y轴分别交于A、C两点，抛物线
经过A、C两点，点B是抛物线与x轴的另一个交点，当
时，y取最大值
.
（1）求抛物线和直线的解析式；
（2）设点P是直线AC上一点，且
，求点P的坐标；
（3）若直线
与（1）中所求的抛物线交于M、N两点，问:
①是否存在a的值，使得∠MON=900？若存在，求出a的值；若不存在，请说明理由；
②猜想当∠MON＞900时，a的取值范围（不写过程，直接写结论）.
（参考公式：在平面直角坐标系中，若M（x1，y1），N（x2，y2），则M，N两点间的距离为
）